Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии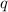 
должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
Графически это выглядит так: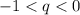 
или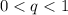 
.
Рассмотрим наши примеры:
1) 
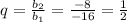. Выполняются ли условия неравенства?
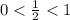. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
2) 
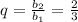. Выполняются ли условия неравенства?
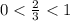. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
3) 
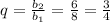. Выполняются ли условия неравенства?
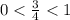. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
Решение системы х=1
у=1
Объяснение:
y=x y=2-x
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблицы:
х -1 0 1 х -1 0 1
у -1 0 1 у 3 2 1
Согласно графиков, они имеют точку пересечения (1; 1) и таблица значений это подтверждает.
Решение системы х=1
у=1
a(n) = a(1) + (n - 1)*d.
По условию, n = 16, a(1) = -7, a(n) = a(16) = 2.
Подставляем и находим d:
2 = -7 + (16 - 1)*d
2 = -7 + 15d
d = 9/15 = 0,6.