(см. объяснение)
Объяснение:
Я так понимаю, нужно объяснить разложение на множители.
Сделать это не так сложно.
Вот пример:
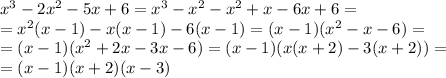
Откуда такие преобразования?
Напишу универсальный алгоритм:
По теореме Безу определить корень уравнения (если корень целый, то он обязательно будет делителем свободного члена (того, что без x)). В нашем один из корней корень x=1.По схеме Горнера или уголком поделить исходный многочлен на x-a, где a - корень уравнения (в нашем случае 1), т.е. делим на (x-1).В результате деления получим (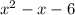
). Первый этап выполнен. Сейчас имеем 
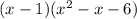.Если уравнение не квадратное, идем на первый этап. Иначе идем на этап 5.Решим уравнение 
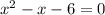(решается либо через дискриминант, либо через теорему Виета). Корни 
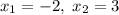.Вспомним формулу: 
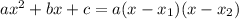. Здесь 
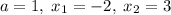. Тогда: 
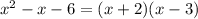.Получили результат: 
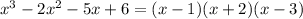.Разложение на множители выполнено!
sinx+sin
2
(x)+sin
3
(x)=cosx+cos
2
x+cos
3
x
(sinx-cosx)+(sin^{2}x-cos^{2}x)+(sin^{3}x-cos^{3}x)=0(sinx−cosx)+(sin
2
x−cos
2
x)+(sin
3
x−cos
3
x)=0
(sinx-cosx)+(sinx-cosx)(sinx+cosx)+(sinx-cosx)(sin^{2}x+sinx*cosx+cos^{2}x)=0(sinx−cosx)+(sinx−cosx)(sinx+cosx)+(sinx−cosx)(sin
2
x+sinx∗cosx+cos
2
x)=0
(sinx-cosx)(1+sinx+cosx+1+sinx*cosx)=0(sinx−cosx)(1+sinx+cosx+1+sinx∗cosx)=0
(sinx-cosx)(2+sinx+cosx+sinx*cosx)=0(sinx−cosx)(2+sinx+cosx+sinx∗cosx)=0
1) sinx=cosxsinx=cosx
tgx=1tgx=1
x= \frac{ \pi }{4} + \pi kx=
4
π
+πk , k∈Z
2) 2+sinx+cosx+sinx*cosx=02+sinx+cosx+sinx∗cosx=0
(1+cosx)(1+sinx)=-1(1+cosx)(1+sinx)=−1 - решений нет, т.к.:
\left \{ {1+cosx \geq 0} \atop {1+sinx \geq 0}} \right.
Левая часть не может быть отрицательной не при каких х.
ответ: x= \frac{ \pi }{4} + \pi kx=
4
π
+πk , k∈Z
Объяснение:
.,,
Вероятность 4%
50:100*8=4