Условие. сумма второго и восьмого членов бесконечно убывающей геометрической прогрессии равна.325/128, а сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой же прогрессии. Найти первый член прогрессии и знаменатель.
Сумма второго и восьмого членов:
Сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой прогрессии:
Из равенства заметим, что второй множитель можно разложить на множители по формуле суммы кубов
Х (км/ч) - собственная скорость баржи х+5 (км/ч) - скорость баржи по течению реки х-5 (км/ч) - скорость баржи против течения реки 48 (ч) - время движения баржи по течению реки х+5 42 (ч) - время движения баржи против течения реки х-5 так как на весь путь баржа затратила 5 часов, то составим уравнение: 48 + 42 =5 х+5 х-5 х≠-5 х≠5 Общий знаменатель:(х-5)(х+5)=х²-25 48(х-5)+42(х+5)=5(х²-25) 48х-240+42х+210=5х²-125 -5х²+90х+95=0 х²-18х-19=0 Д=18²+4*19=324+76=400 х₁=18-20 = -1 - не подходит по смыслу задачи 2 х₂= 38 =19 (км/ч) - собственная скорость баржи 2 ответ: 19 км/ч
Условие. сумма второго и восьмого членов бесконечно убывающей геометрической прогрессии равна.325/128, а сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой же прогрессии. Найти первый член прогрессии и знаменатель.
Сумма второго и восьмого членов: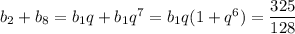
Сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой прогрессии:
Из равенства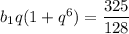 заметим, что второй множитель можно разложить на множители по формуле суммы кубов
заметим, что второй множитель можно разложить на множители по формуле суммы кубов
Подставляем данные, получим
ответ: 5; 0.5 и -5; -0.5.