Question

решить, будет сложный тест по функциям, нужно понять, как сделать

Answer 1

1) y(x) = $\sqrt{x}$

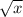
y(0.5) =$\sqrt{0.5}$

 y(0.5) ≈ 0.7

y(1.5) = $\sqrt{1.5}$

 y(1.5) ≈ 1.2

y(2.5) =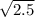 $\sqrt{2.5}$

 y(2.5) ≈ 1.6

2) x(y) = $y^{2}$

y(0.5) = $0.5^{2}$

 y(0.5) = 0.25

y(1.5) =  $1.5^{2}$

 y(1.5) = 2.25

y(2.5) = $2.5^{2}$

 y(2.5) = 6.25

Объяснение:

Функция Y при X = чемуто обозначается y(x) где x это указанное число. Пример: y при x, равном 3 - y(3). Далее подставляешь.

Функция X при Y = чемуто обозначается x(y) где y это указанное число. Пример: y при x, равном 3 - x(3). Далее меняешь функцию Y под X =.

y(x) =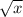 $\sqrt{x}$ это x(y) = $y^{2}$