y = -3x² + 12x + 3
а)
график функции пересекает ось ОУ при х = 0, значит:
y = -3x² + 12x + 3,
у = -3*0² + 12*0 + 3,
у = 3 ⇒ (0; 3) - точка пересечения графика с осью ОУ,
б)
график функции пересекает ось ОХ при у = 0, значит:
y = -3x² + 12x + 3,
0 = -3х² + 12х + 3,
х² - 4х - 1 = 0,
Д = (-4)² - 4*1*(-1) = 16 + 4 = 20,
х1 = (4 + √20) / 2*1 = (4 + 2√5)/2 = 2 + √5,
х2 = (4 - √20) / 2*1 = (4 - 2√5)/2 = 2 - √5 ⇒
(2+√5; 0) и (2-√5; 0) - точки пересеч. графика с осью ОХ,
с)
уравнение оси симметрии к графику функции y = ax²+bx+c имеет вид:
x = -b/(2a)
(т.е. прямая параллельная оси ординат и проходящая через вершину параболы)
Для данной функции a = -3, b = 12, c = 3, значит
уравнение оси симметрии:
x = -12 / (2*(-3)) = -12 / (-6) = 2,
х = 2,
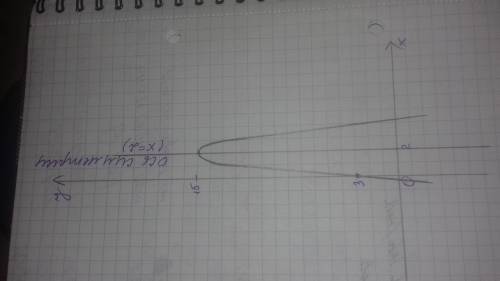
д)
график на фото:
1) Это формула квадрата суммы: (x+3)^2>=0, здесь х - любое число, так как квадрат любого выражения всегда неотрицательное число. ответ: (-беск; +беск)
2) Приводим подобные: 1,5х-4<0. 1,5x<4, делим на 1,5=3/2: x<(4*2)/3, x<8/3,
x<2целых 2/3, т.е. ответ (-беск; 2целых2/3)
3) 2x^2<=x, 2x^2 -x<=0, x(2x-1)<=0. Метод интервалов. x(2x-1)=0, отсюда
х=0 или 1/2/ Наносим на числовую прямую найденные числа и расставляем знаки. Получим: на промежутке (-беск; 0] знак "-" , на промежутке [0; 1/2] знак "+" б
на промежутке [1/2; +беск) знак "-". Нам нужен промежуток с минусом. Это
[0; 1/2]