∉ и И
Объяснение:
Во первых множество всех натуральных чисел обычно обозначают буквой N.
2. Если к натуральным числам присоединить число 0 и все целые отрицательные числа: −1,−2,−3,−4... — то получится множество целых чисел. Это множество обычно обозначают буквой Z.
3. Если к множеству целых чисел присоединить все обыкновенные дроби, то получится множество рациональных чисел. Это множество обычно обозначают буквой Q.
4. ∈ — знак принадлежности (элемент принадлежит множеству).
5. ∉ — элемент не принадлежит множеству.
1 Центр(2;-4) , радиус равен 2
2 центр имеет координаты (-1+3)/2=1;у=(3+3)/2=3, т.е. центр (1;3), а радиус равен √(16+0²)/2=4/2=2
3. с осью оу х=0, у=3, это точка (0;3), с осью ох у=0, х=12, это точка (12;0)
подставим у =х-2 в первое уравнение х+4у-12=0 . получим
х+4х-8-12=0, откуда 5х=20, х=4, тогда у=4-2=2.
итак. получили точку пересечения (4;2)
4. подставим у=-х+4 в первое уравнение окружности. получим
(х-2)² + (-х+4-4)² =2 ⇒х²-4х+4+х²=2; 2х²-4х+2=0; х²-2х+1=0; ⇒(х-1)²=0, х=1, у=4-1=3. искомая точка (3; 1)
1)2x³-x³+7x2+x-4x²-5х=2x³-x³+14+x-4x²-5x=x³+14-4x-4x²=x³-4x²-4x+14 при х=2
2³-4*2²-4*2+14=8-2⁴-8+14=8-16-8+14=-2
2) 0,46³ -0,26² +0,56 -0,363-0,56+7=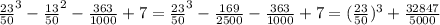 ≈6.666736
≈6.666736
3) -4a²b+3ab2 +3a²b-5ab2+5а²b=4a²b+3ab2-5ab2=4a²b-2ab2=4a²b-4ab=4ab(a-1) при а=5 b=-0.4=4*5*(-0.4)(5-1)=4*5(-0.4)*4=-32
4) -0,3x-13xy2-37ху²=-0,3x-(13*2)xy-37xy²=-0,3x-26xy-37xy² при х=4 у=-0,2 =-0,3*4-26*4*(-0,2)-37*4*(-0,2)²=4(-0,3+26*0,2-37*(-0,2)²)=4(-0,3+5,2-37*0,2²)=4(-0,3+5,2-37*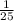 )=4(-0,3+5,2-
)=4(-0,3+5,2-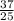 )=4(-0,3+5,2-1,48)=4*3,42=13,68
)=4(-0,3+5,2-1,48)=4*3,42=13,68
Объяснение: