Решим уравнение
х2 + 10х - 24 = 0.
Разложим левую часть на множители:
х2 + 10х - 24 = х2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х - 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10х Метод выделения полного квадрата.
Решим уравнение х2 + 6х - 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2• х • 3.
В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как
х2 + 2• х • 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнения
х2 + 6х - 7 = 0,
прибавляя к ней и вычитая 32. Имеем:
х2 + 6х - 7 = х2 + 2• х • 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 - 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 - 4 = 0, х1 = 1, или х + 3 = -4, х Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) - b2 + 4ac = 0,
(2ax + b)2 = b2 - 4ac,
2ax + b = ± √ b2 - 4ac,
2ax = - b ± √ b2 - 4ac,
Примеры.
а) Решим уравнение: 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 - 4ac = 72 - 4 • 4 • 3 = 49 - 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b2 - 4ac >0 , уравнение ах2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х2 - 4х + 1 = 0,
а = 4, b = - 4, с = 1, D = b2 - 4ac = (-4)2 - 4 • 4 • 1= 16 - 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 - 4ac = 0, то уравнение
ах2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b2 - 4ac = 32 - 4 • 2 • 4 = 9 - 32 = - 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b2 - 4ac < 0,
уравнение ах2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 +x2 = - p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например,
x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = - 3 < 0;
x2 + 8x + 7 = 0; x1 = - 7 и x2 = - 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
Например,
x2 + 4x – 5 = 0; x1 = - 5 и x2 = 1, так как q= - 5 < 0 и p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1, так как q = - 9 < 0 и p = - 8 < 0.
Объяснение:
Прочитай это, потом поймёшь.
Объяснение: Щоб знайти найбільше і найменше значення функції на відрізку, треба
а) знайти максимуми і мінімуми функції на цьому відрізку. Для цього беруть похідну і прирівнюють її до 0. Рішення і є критичними точками.
б) знайти значення функції на кінцях відрізку.
в) вибрати найбільше і найменше значення функції.
3. а) g'(x)=(-x²+6x-1)'= -2x+6
g'(x)=0, -2x+6=0, -2x=-6, x=3
g(3)= -3²+6·3-1=-9+18-1=8, g(3)=8
б) [2;4]
g(2)=-2²+6·2-1=-4+12-1=7, g(2)=7
g(4)=-4²+6·4-1=-16+24-1=7, g(4)=7
в) Найбільше значення функції g(3)=8
Найменше значення функції g(2)=7 і g(4Объяснение: Щоб знайти найбільше і найменше значення функції на відрізку, треба
а) знайти максимуми і мінімуми функції на цьому відрізку. Для цього беруть похідну і прирівнюють її до 0. Рішення і є критичними точками.
б) знайти значення функції на кінцях відрізку.
в) вибрати найбільше і найменше значення функції.
3. а) g'(x)=(-x²+6x-1)'= -2x+6
g'(x)=0, -2x+6=0, -2x=-6, x=3
g(3)= -3²+6·3-1=-9+18-1=8, g(3)=8
б) [2;4]
g(2)=-2²+6·2-1=-4+12-1=7, g(2)=7
g(4)=-4²+6·4-1=-16+24-1=7, g(4)=7
в) Найбільше значення функції g(3)=8
Найменше значення функції g(2)=7 і g(4)=7
7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)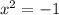
число в корне не может равняться отрицательному числу, корней уравнения нет.
2)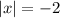
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)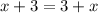
корней уравнения нет.
2)
корней уравнения нет.
=> уравнения равносильные.
9. 1)
ОДЗ: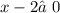 ,
, 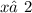 ;
;
ответ:
2)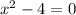
ответ: ;
; 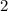
=> уравнения не равносильные.
10. 1)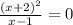
ОДЗ: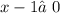 ,
, 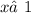 ;
;
ответ:
2)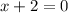
ответ:
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12.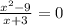
ОДЗ: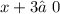 ,
,  ;
;
ответ: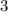
13.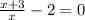
ОДЗ: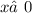 ;
;
ответ: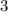
14.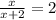
ОДЗ: ,
,  ;
;
ответ: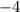
15.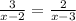
ОДЗ: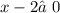 ,
, 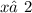 ,
, 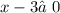 ,
,  ;
;
ответ:
16.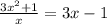
ОДЗ: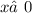 ;
;
ответ: