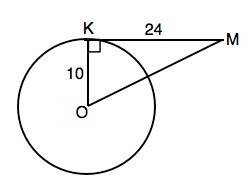
Обозначим центр окружности О, точку касания К.
Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∆ МОК - прямоугольный.
Отношение катетов 10:24=5:12 указывает на то, что длины сторон треугольника из Пифагоровых троек 5:12:13, в которых эти длины –целые числа.⇒ МО=2•13=26. И это можно проверить по т.Пифагора.
МО=√(KO²+KM²)=√676=26
В прямоугольном треугольнике каждый катет является высотой, проведенной к другому катету.
Площадь прямоугольного треугольника равна половине произведения катетов:
S=КМ•КО:2=24•10:2=120 см²
По условию известно, что режимов освещения было не больше 5. То есть их могло быть:
1, 2, 3, 4, 5
Так как существует также полное отключение освещения, всего состояний может быть:
2, 3, 4, 5, 6
Найдем, сколько раз нужно нажать на кнопку, чтобы независимо от точного количества режимов вернуться в тот же самый режим. Для этого, нужно найти число, которое делится на 2, 3, 4, 5, 6 без остатка. То есть, другими словами нужно найти НОК этих чисел.
Таким образом, если нажать на кнопку 60 раз, то мы перейдем к такому же состоянию, с которого все начиналось.
По условию сейчас включен первый режим, также известно, что именно перед первым режимом идет состояние полного отключения. Значит, нажав на кнопку 60 раз мы вернемся к первом режиму, а если мы нажмем на кнопку на 1 раз меньше, то есть 59 раз, то мы полностью выключим свет.
Найденный является простейшим с той точки зрения, что нажать на кнопку можно и большее количество раз, а именно любое количество, задаваемое формулой , где
, где 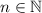 , и свет также будет отключен.
, и свет также будет отключен.
ответ: нажать на кнопку 59 раз