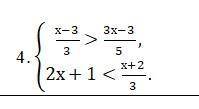

1-ое уравнение:
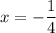
2-ое уравнение:
Объяснение:
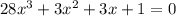
разложение на множители):
Заметим, что данное уравнение хорошо раскладывается на множители:
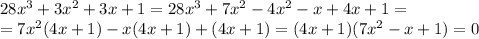
Второй множитель не имеет корней.
Поэтом ответ 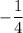 .
.
Поделим исходное уравнение на 28. Получим:
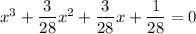 , где
, где 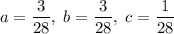
Выполним вычисления:
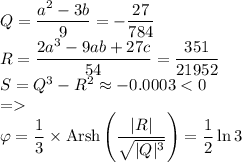
Тогда действительный корень будет равен:
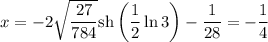
Пришли к тому же ответу.
Уравнение решено!
2)
(x²+4x)(x²+x-6)=(x³-16x)(x²-2x-35)
Раскроем скобки и упростим вырождение:
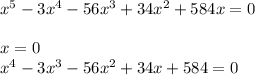
Второе уравнение раскладывается на множители:
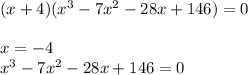
Последнее кубическое уравнение не имеет целых корней.
Поэтому нужно считать так же, как мы делали это при решении 1-ого уравнения 2-ым
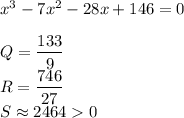
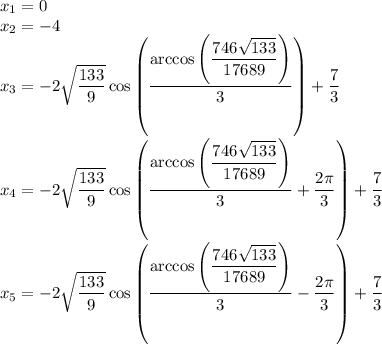
Значит имеем 3 корня:
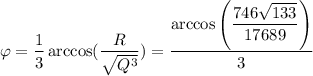
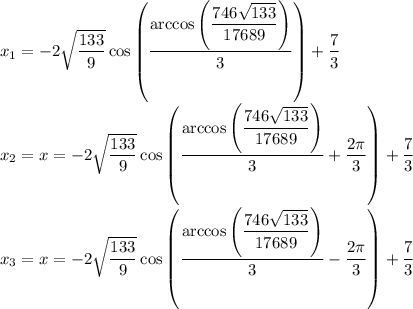
Итого, уравнение имеет 5 корней:

Задание выполнено!
ответ: 8) n=4 или n=5
Объяснение:
дробь правильная, если числитель меньше знаменателя...
n²-n+15 < 7n+3
n²-8n+12 < 0 корни по т.Виета (2) и (6);
решение "между корнями": n ∈ (2; 6),
т.е. n∈N (по условию) может быть равно: {3; 4; 5}
остальное (сократима ли дробь) проще посчитать...
n=3: 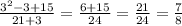 дробь сократима...
дробь сократима...
n=4: 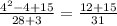 дробь НЕсократима (31-простое число))
дробь НЕсократима (31-простое число))
n=5: 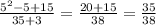 дробь НЕсократима...
дробь НЕсократима...
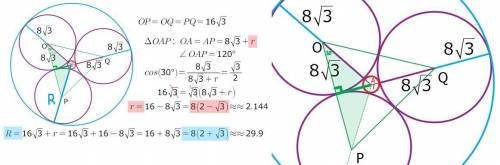
решение задачи 9) на рисунке...
таких окружностей две...
касание может быть как внутренним, так и внешним...
точки касания окружностей лежат на линии центров...
niger
Объяснение:
выeb negra eto hofotho