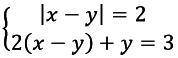
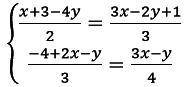
1. 1) если х-у<0, то -х+у=2, откуда у=2+х, подставим во второе уравнение, получим 2*(х-(х+2))+х+2=3; 2х-2х-4+х+2=3; х=5, значит, у=2+5=7; проверим х-у<=5-7=-2; подходят, значит, решение системы х=5; у=7, или же точка (5;7)
2) если х-у≥0, то х-у=2, откуда у=х-2, подставим во второе уравнение, получим 2*(х-(х-2))+х+2=3; 2х-2х+4+х-2=3; х=1, значит, у=1-2=-1; проверим
х-у<=1-(-1)=2; подходят, значит, решение системы х=1; у=-1, или же точка (1;-1)
ответ: 1. (5;7); (1;-1)
2. приведем к общему знаменателю, в первом уравнении это 6, во втором 12, т.к. знаменатели взаимно просты, то НОЗ этих знаменателей - их произведение.
упростим первое уравнение, 3*(х+3-4у)=2*(3х-2у+1); 3х+9-12у=6х-4у+2;
-8у-3х=-7;
упростим второе уравнение 4*(-4+2х-у)=3*(3х-у); -16+8х-4у=9х-3у;
х+у=-16.
Получили упрощенную систему
х+у=-16
-3х-8у=-7, умножим первое уравнение на 3 и сложим со вторым, получим
3х+3у=-48
-3х-8у=-7, после сложения -5у=-55; у=11, подставим в уравнение х+у=-16, получим х+11=-16, откуда х=-27, значит, решение системы - точка (-27;11)
ответ х=-27; у=11
1) по двум катетам: а) а = 3, b = 4; б) a = 9, b = 40; в) a = 20, b = 21; г) a = 11, b = 60; 2) по гипотенузе и катету: а) с = 13, a =-5; б) с = 25, a = 7; в) a = 17, а = 8; г) с = 85, a = 84; 3) по гипотенузе и острому углу: а) с = 2, a = 20°; б) с = 4, a = 50°20’ в) с = 8, a = 70°36’ г) с = 16, a = 76°21’ 4) по катету и противолежащему углу: а) а = 3, a = 30°27’ б) а = 5, a = 40°48’ в) а = 7, a = 60°85’ г) а = 9, a = 68°’.
1) По двум катетам: а) а = 3; b = 4;
По гипотенузе и катету: а) с = 13; а = 5.
ответ: 1400 см².
Объяснение:
Пусть a и b - меньшая и большая боковые стороны трапеции, c и d - меньшее и большее основания трапеции, α и β - тупой и острый углы трапеции. По условию, b=50 см, с=20 см. Тогда площадь трапеции S=a*c+(d-c)*a/2 см². По теореме Пифагора, a²+(d-c)²=b²=50²=2500 см². Кроме того, a/c=a/20=tg(α/2), а a/b=a/50=sin(β). Но так как α+β=180°, то β=180°-α и тогда a/50=sin(180°-α)=sin(α). Мы получили систему уравнений:
a/20=tg(α/2)
a/50=sin(α).
Но так как sin(α)=2*sin(α/2)*cos(α/2)=2*tg(α/2)*cos²(α/2), то отсюда следует уравнение a/50=2*a/20*cos²(α/2), или 1=5*cos²(α/2). Отсюда cos²(α/2)=1/5 и cos(α)=2*cos²(α/2)-1=2/5-1=-3/5. Используя основное тригонометрическое тождество sin²(α)+cos²(α)=1 и учитывая, что sin(a)>0, находим sin(α)=√[1-cos²(α)]=√16/25=4/5. Отсюда a=50*sin(α)=50*4/5=40 см, d-c=√(b²-a²)=√900=30 см и S=40*20+30*40/2=1400 см².
№1
(1;-1), (5;7)
№2
(-27;11)
Объяснение:
Всё в файлике