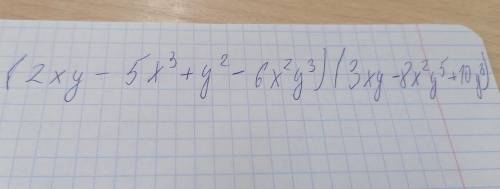
{
x−y=1
x+y=9
⇔{
y=x−1
y=9−x
Графики линейных функций y = 9–x и y = x–1 - прямые. Для построения графика прямой достаточно 2 точки, через которых проходит эта прямая. Находим эти точки из уравнения функций.
Для функции y = 9–x (зелёные точки):
1) x=0 ⇒ y= 9–0= 9 ⇒ (0; 9)
2) y=0 ⇒ 0= 9–x ⇒ x= 9 ⇒ (9; 0).
Для функции y = x–1 (синие точки):
1) x=0 ⇒ y= 0–1= –1 ⇒ (0; –1)
2) y=0 ⇒ 0= x–1 ⇒ x= 1 ⇒ (1; 0).
Построим графики функций в одной системе координат (см. рисунок 1). Из рисунка определяем точку пересечения графиков функций (красная точка и красные штрихи):
(5; 4).
\tt \displaystyle \left \{ {{3 \cdot x+y=1} \atop {x+y=5}} \right. \Leftrightarrow \left \{ {{y=1-3 \cdot x} \atop {y=5-x}} \right.{
x+y=5
3⋅x+y=1
⇔{
y=5−x
y=1−3⋅x
Графики линейных функций y = 1–3•x и y = 5–x - прямые. Для построения графика прямой достаточно 2 точки, через которых проходит эта прямая. Находим эти точки из уравнения функций.
Для функции y = 1–3•x (синие точки и синие штрихи):
1) x=0 ⇒ y= 1–3•0 = 1 ⇒ (0; 1)
2) x=1 ⇒ y= 1–3•1 = –2 ⇒ (1; –2).
Для функции y = 5–x (зелёные точки):
1) x=0 ⇒ y= 5–0 = 5 ⇒ (0; 5)
2) y=0 ⇒ 0= 5–x ⇒ x= 5 ⇒ (5; 0).
Построим графики функций в одной системе координат (см. рисунок 2). Из рисунка определяем точку пересечения графиков функций (красная точка и красные штрихи):
(–2; 7).
\tt \displaystyle \left \{ {{y-6 \cdot x=-25} \atop {y-x=-5}} \right. \Leftrightarrow \left \{ {{y=6 \cdot x-25} \atop {y=x-5}} \right.{
y−x=−5
y−6⋅x=−25
⇔{
y=x−5
y=6⋅x−25
Графики линейных функций y = 6•x–25 и y = x–5 - прямые. Для построения графика прямой достаточно 2 точки, через которых проходит эта прямая. Находим эти точки из уравнения функций.
Для функции y = 6•x–25 (синие точки и синие штрихи):
1) x=2 ⇒ y= 6•2–25 = –13 ⇒ (2; –13)
2) x=3 ⇒ y= 6•3–25 = –7 ⇒ (3; –7).
Для функции y = x–5 (зелёные точки):
1) x=0 ⇒ y= 0–5 = –5 ⇒ (0; –5)
2) y=0 ⇒ 0= x–5 ⇒ x= 5 ⇒ (5; 0).
Построим графики функций в одной системе координат (см. рисунок 3). Из рисунка определяем точку пересечения графиков функций (красная точка и красные штрихи):
(4; –1).
В решении.
Объяснение:
раскрыть скобки привести подобные слагаемые:
(2xy - 5x³ + у² - 6x²y³)*(3xy - 8x²y⁵ + 10y⁸) =
= 6х²у² - 16х³у⁶ + 20ху⁹ - 15х⁴у + 40х⁵у⁵ - 50х³у⁸ + 3ху³ - 8х²у⁷ + 10у¹⁰ -
- 18х³у⁴ + 48х⁴у⁸ - 60х²у¹¹.
Нет подобных слагаемых.