Решением является перебор вариантов:
Можно достать шары из урны четырьмя
1) 2 белых
2) 2 чёрных
3) 1 белый и 1 чёрный
4) сначала 1 чёрный, потом 1 белый.
Вероятности этих событий:
1) 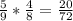
2) 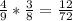
3) 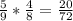
4) 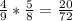
Вероятность того, что мы достанем из урны два одинаковых по цвету шара равна сумме вероятностей в первом и во втором случаях:
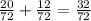
Вероятность вынимания шаров разных цветов (не важно в какой последовательности) равна сумме вероятностей в третьем и в четвёртом случаях:
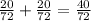
Сравнивая две полученные дроби мы приходим к выводу, что вынуть два разных по цвету шара более вероятнее, чем два одинаковых.
ответ:![x \in [1; \ 5]](/tpl/images/0205/7464/e62de.png)
ОДЗ: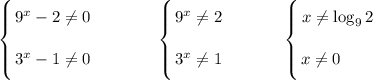
Замена: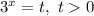
ОДЗ:
По методу интервалов выясняем знаки неравенства и получаем:
Обратная замена:
Объединяем все три условия и получаем:
ответ:![x \in \bigg[\log_{3}\dfrac{1}{2}; \ 0 \bigg) \cup (\log_{3}\sqrt{2}; \ 1]](/tpl/images/0205/7464/ef558.png)