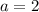
Объяснение:
Так, сначала восстановим меньшие коэффициенты  и
и  , а затем займёмся старшим коэффициентом
, а затем займёмся старшим коэффициентом  .
.
Начнём с коэффициента  . Как мы видим при
. Как мы видим при 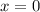 ,
, 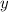 принимает значение
принимает значение  . Это значит, что свободный член (коэффициент
. Это значит, что свободный член (коэффициент  ) равен
) равен  .
.
Однако, есть ещё одна интересная деталь. При 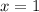 ,
, 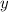 также принимает значение
также принимает значение  . Если мы подставим в уравнение
. Если мы подставим в уравнение 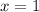 , то получим вот что:
, то получим вот что:
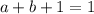 . Это означает, что коэффициенты
. Это означает, что коэффициенты  и
и 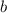 равны по значению, но противоположны по знаку. Иными словами:
равны по значению, но противоположны по знаку. Иными словами: 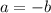 .
.
Координаты вершины параболы судя по графику 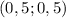 . И если с координатой абсцисс мы уже разобрались в наших логических рассуждениях, то нахождение координаты ординат нам выйти на коэффициенты
. И если с координатой абсцисс мы уже разобрались в наших логических рассуждениях, то нахождение координаты ординат нам выйти на коэффициенты  и
и 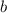 .
.
Так как  по числовой характеристике равно
по числовой характеристике равно 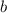 , то мы можем вместо
, то мы можем вместо 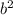 использовать
использовать 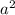 (так как отрицательное число в квадрате будет положительное число).
(так как отрицательное число в квадрате будет положительное число).
Координата ординаты вершины параболы вычисляется по формуле:
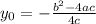
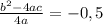
Найдём наконец коэффициент 
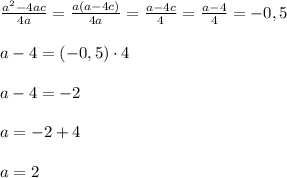
Теперь мы кстати можем восстановить функцию полностью:
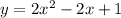
a) х=(-8)
y=1/2×(-8)+2
y= (-2)
б) y=(-10)
(-10)=1/2×X+2
(-12)=1/2×X
X=(-12)÷1/2
X=(-24)
в)X=(-16)
Y=(-6)
(-6)=1/2×(-16)+2
(-6)=(-6)
точка В проходит через эту функцию.
Объяснение:
а) т.к аргумент-это значение Х,то мы просто подставляем значение Х=(-8) и находим значение Y(Функции)
б) Т.к значение функции -это значение Y,то мы аналогичным образом подставляем значение Y=(-10) и находим значение X(аргумента)
в) Точка В(-16;-6)
в координатах точки сначала стоит значение Х , а затем значение Y
Соответственно Х=(-16)
Y=(-6)
подставляем эти значения в формулу функции
если левая часть равно правой , то функция проходит через эту точку.
правильный ответ
Объяснение:
это правильно