Question

нужно показать дз уже завтра вместо знака бесконечности пишите & или лучше просто отправьте фото буду очень благодарен

Answer 1

$1)\ \ f(x)=3x-x^2\\\\f(0)=3\cdot 0-0^2=0\\\\f(1)=3\cdot 1-1^2=3-1=2\\\\f(2)=3\cdot 2-2^2=6-4=2\\\\\\2)\ \ g(x)=\dfrac{x+3}{x-1}\ \ ,\ \ ODZ:\ x\ne 1\ ,\\\\g(0)=\dfrac{0+3}{0-1}=\dfrac{3}{-1}=-3\\\\g(2)=\dfrac{2+3}{2-1}=\dfrac{5}{1}=5\\\\g(-3)=\dfrac{-3+3}{-3-1}=\dfrac{0}{-4}=0$

Answer 2

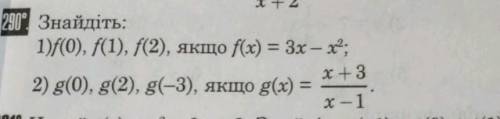
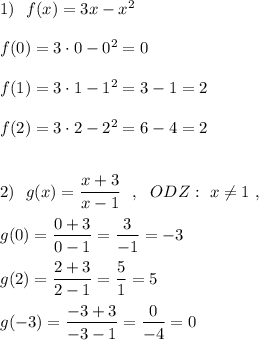
В решении.

Объяснение:

1) Дана функция f(x) = 3x - x²;

а) Найти f(0);  f(1);  f(2);

f(0) = 3 * 0 - 0² = 0;

f(1) = 3 * 1 - 1² = 2;

f(2) = 3 * 2 - 2² = 6 - 4 = 2.

б) Найти область определения функции.

f(x) = 3x - x²

Уравнение квадратичной функции, значит, график - парабола.

3x - x² = 0

-х² + 3х = 0

х² - 3х = 0, неполное квадратное уравнение.

х(х - 3) = 0

х₁ = 0;

х - 3 = 0

х₂ = 3.

Ветви параболы направлены вниз, пересекают ось Ох в точках х = 0;  

х = 3.

Область определения - это проекция графика функции на ось Ох.

Обозначается как D(f) или D(у).  

Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.

Обычно запись: D(f) = R.

2) Дана функция g(x) = (x + 3)/(x - 1);

а) Найти g(0);  g(2);  g(-3);

g(0) = (0 + 3)/(0 - 1) = -3;

g(2) = (2 + 3)/(2 - 1) = 5;

g(-3) = (-3 + 3)/(-3 - 1) = 0.

б) Найти область определения функции.

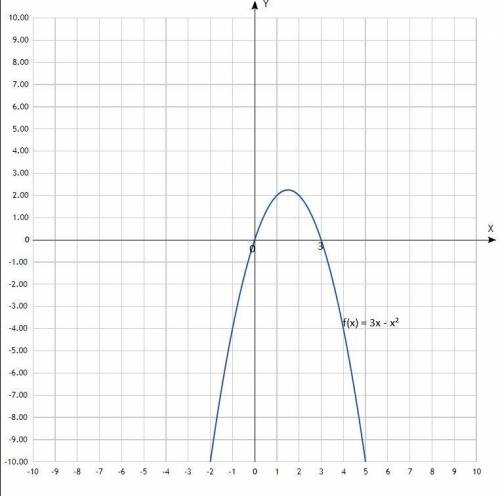
Судя по уравнению, график функции - гипербола.

Чтобы данное уравнение функции имело смысл, знаменатель дроби не должен быть равен 0, а значение х ≠ 1.

Значит, область определения функции - множество всех действительных чисел, только х ≠ 1.

Запись: D(f) = х∈R : х ≠1.