 - длина, тогда
- длина, тогда 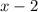 - ширина. Проведём диагональ в прямоугольнике, получаем прямоугольный треугольник. Исходя из этого мы получаем уравнение по теореме Пифагора.
- ширина. Проведём диагональ в прямоугольнике, получаем прямоугольный треугольник. Исходя из этого мы получаем уравнение по теореме Пифагора.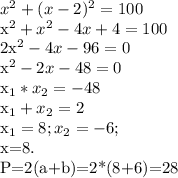
 - катет CB, тогда гипотенуза AB -
- катет CB, тогда гипотенуза AB -  . Составим уравнение по теореме Пифагора.
. Составим уравнение по теореме Пифагора.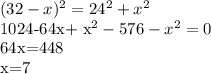
 - большее число, тогда
- большее число, тогда 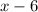 - меньшее число. Составим уравнение, зная произведение этих чисел.
- меньшее число. Составим уравнение, зная произведение этих чисел.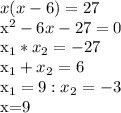
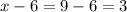 .
.
Объяснение:
Д=7²-4*4*(-15)=289
х1=
(-7+√289)//(2*4)=10/8=1.25
х2=(-7-17)/8=-3
сумма 1.25+(-3)=-1.75
произведение 1.25*(-3)=-3.75