Координаты точек пересечения графиков функций (параболы и прямой линии) (1; 1); (3; 9).
Объяснение:
Построить в одной системе координат графики функций и найти координаты точек их пересечения: y=x² и y=4x-3.
Первый график парабола с вершиной в начале координат, второй прямая линия.
Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y=x² y=4x-3
Таблицы:
х -3 -2 -1 0 1 2 3 х -1 0 1
у 9 4 1 0 1 4 9 у -7 -3 1
Согласно графика, координаты точек пересечения графиков функций (параболы и прямой линии) (1; 1); (3; 9).
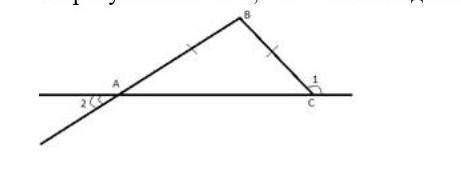
180 - ∠1
Объяснение:
Т.к АВС равнобедренный (по условию) то и углы BAC и BCA равны.
Угол BCA = 180 - ∠1, т.к они смежные, отсюда находим и ∠BAC, который является вертикальным к углу 2, т.е равным ему.
Отсюда:
∠2 = 180 - ∠1