Полное условие смотри в приложении.
а)
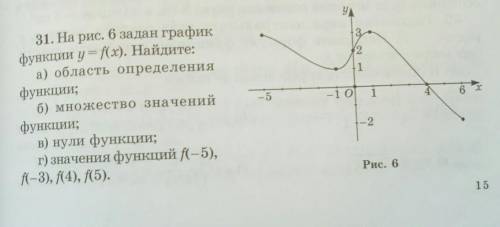
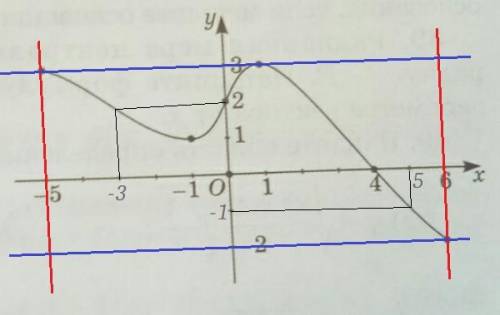
На графике область определения это множество значений, которые принимают x, для этого графика. Видно, что -5 ≤ x ≤ 6.
ответ: D(f) = [-5;6].
б)
Множеством значений, будет множество для y. -2 ≤ y ≤ 3.
ответ: E(f) = [-2;3].
в)
Нули функции это координата точки пересечения графика с осью Ox, по оси Ox. Точка: (4;0), координата по оси Ox: 4.
ответ: x = 4.
г)
Необходимо найти значение (y) функции f(x) для данных аргументов (x). Определяем точку графика с соответствующим x, а затем находим для неё y.
ответ: f(-5) = 3; f(-3) = 2; f(4) = 0; f(5) = -1.
. Сейчас мы рассмотрим правила нахождения значений выражений. Начнем с числовых выражений, и будем продвигаться от самых простых случаев, когда выражение содержит лишь числа и соединяющие их знаки арифметических действий, и закончим общим случаем, когда в выражении, значение которого нужно найти, содержатся скобки, дроби, корни, степени и другие функции. В конце покажем, как находить значения буквенных выражений и выражений с переменными при выбранных значениях переменных. Всю теорию снабдим примерами с подробным описанием решений.
(8,15*1.85)+1.85*1.85=15.0775+3.4225
15.0775+3.4225=18.5