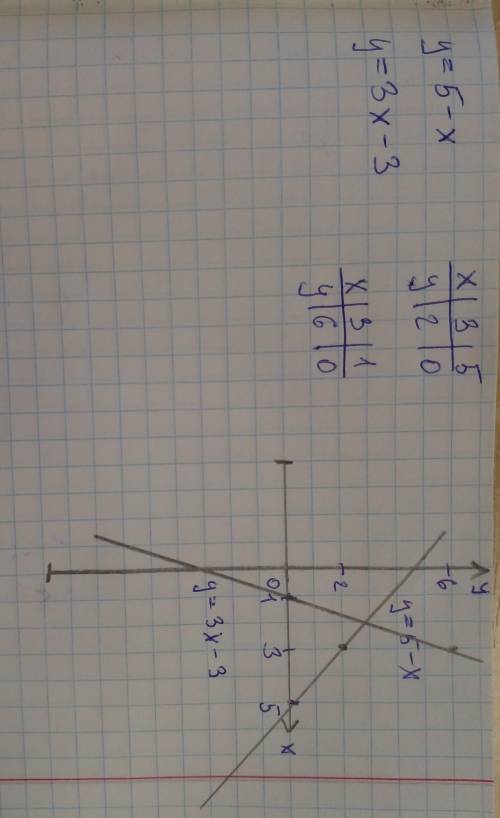
данные графики пересекаются
Объяснение:
так как коэфициент k не совпадает
1) Квадратным уравнением называют уравнение ax^2+bx+c=0, где x — переменная, a, b и c — действительные числа, причем a не равно 0.
При этом a называют старшим или первым коэффициентом, b — вторым коэффициентом, c — свободным членом.
2) полные
неполные
приведённые
3) Корни квадратного уравнения ax^2+bx+c=0 находятся по формуле:
x=-b±√D/2a, где D^2-4ac - дискриминант квадратного уравнения
4)Если дискриминант больше нуля, то квадратное уравнение имеет два различных действительных корня.
Если дискриминант равен нулю, то квадратное уравнение имеет только один действительный корень, или, что то же самое - два равных действительных корня, которые равны.
5) Приведённое квадратное уравнение - это квадратное уравнение, у которого первый коэффициент равен 1.
Квадратное уравнение вида x^2+px+q=0 называется приведённым.
Квадратное уравнение называют приведённым, если его коэффициент равен 1
Даны координаты вершин пирамиды:
А1 (-10; 6; 6), А2 (-2; 8; 2), А3 (5; -7; 4), А4 (-4; 10; 9).
Найти:
1) угол между ребрами А1А2 и А1А4.
Находим векторы А1А2 и А1А4.
А1А2 = (-2-(-10); 8-6; 2-6) = (8; 2; -4), модуль равен √(64+4+16) = √84 = 2√21.
А1А4 = (-4-(-10); 10-6; 9-6) = (6; 4; 3), модуль равен √(36+16+9) = √61.
Находим косинус угла (А1А2_А1А4):
cos (А1А2_А1А4) = (8*6+2*4+(-4)*3)/( 2√21*√61) = 44/(2√1281) = 22√1281/1281.
Угол (А1А2_А1А4) = arccos(22√1281/1281) = arccos 0,614679 = 0,90882 радиан или 52,0714 градуса.
2) уравнение прямой А1А2.
По точке А1 (-10; 6; 6) и вектору А1А2(8; 2; -4) составляем уравнение:
(x + 10)/8 = (y – 6)/2 = (z – 6)/(-4).
ты в каком классе это надо