D (область определения) ∈ (+∞ : -∞)
Е (область значений) ∈ [11 ; -∞)
Объяснение:
область определения - это все значения х
область значений функции - это все у
По условию дано: f (x) = -х² + 6х + 2, высчитаем максимальный у (у данного графика есть у максимальное, так как ветви параболы направлен вниз), для этого нужно найти х вершины по формуле:
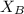 = -b/2a = -6/-2 = 3,
= -b/2a = -6/-2 = 3,
подставим это значение х в функцию и найдём у:
f (x) = -х² + 6х + 2 = -9 + 18 + 2 = 11
=> Е (область значений) ∈ [11 ; -∞)
в то время как D (область определения) ∈ (+∞ : -∞)
1.Найти экстремумы функций:
1) f(x)=х^3-х^2-х +2 2) f(x)= (8 -7х)*е^х
2.Найти интервалы возрастания и убывания функции f(x)=х^3-х^2-х +2
1
1)f`(x)=3x²-2x-1=0
D=4+12=16
x1=(2-4)/6=-1/3
x2=(2+4)/6=1
+ _ +
(-1/3)(1)
max min
ymax=-1/27-1/9+1/3+2=(-1-3+9+54)/27=59/27
ymin=1-1-1+2=1
2)f`(x)=-7e^x+(8-7x)e^x=e^x*(-7+8-7x)=0
1-7x=0
x=1/7
+ _
(1/7)
max
ymax=(8-1)*e^(1/7)=e^(1/7)
2
f`(x)=3x²-2x-1=0
D=4+12=16
x1=(2-4)/6=-1/3
x2=(2+4)/6=1
+ _ +
(-1/3)(1)
возр убыв возр
3
смотреть 1
x=-1/3∈[-1;3/2]
x=1∈[-1;3/2]
y(-1)=-1-1+1+2=1
y(-1/3)=59/27 наиб
4
y(1)=1
y(3/2)=27/8-9/4-3/2+2=(27-27-12+16)/8=1/2 наим
5
f`(x)=3x²-2x-1
f``(x)=6x-2 прямая проходит через точки (0:-2) и (1;4)