
Биквадратное уравнение.
Решается заменой переменной:

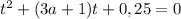
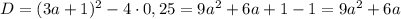
Если D >0, т.е.


уравнение имеет корни:
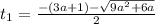 или
или 
Обратный переход:
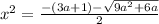 или
или 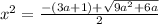
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
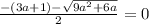
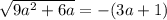
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
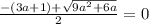
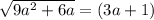
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 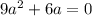
 или
или 
При 
уравнение принимает вид:

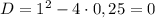 ⇒
⇒ 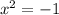
уравнение не имеет корней
При 
уравнение принимает вид:

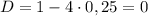 ⇒
⇒ 
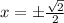
Уравнение 4-ой степени, значит
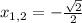 и
и 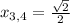
О т в е т. При 
Объяснение:
1. ОДЗ: х ∈ R.
2. Четность, нечетность.
⇒ функция не является четной или нечетной, то есть общего вида.
3. Пересечение с осями.
(корни найдены с онлайн калькулятора)
4. Функция непрерывна, асимптот не имеет.
5. Возрастание, убывание, точки экстремумов.
Найдем производную, приравняем к 0. Найдем корни, отметим их на числовой оси и определим знак производной на промежутках.
Если "+" - функция возрастает, "-" - убывает.
Функция возрастает при х ∈ (-∞; -1] ∪ [1; +∞)
Функция убывает при х ∈ [-1; 1]
См. рис.
6. Выпуклость, вогнутость, точки перегиба.
Найдем производную второго порядка, приравняем к 0. Найдем корни, отметим их на числовой оси и определим знак второй производной на промежутках.
Если "+" - функция вогнута, "-" - выпукла.
Функция выпукла при х ∈ (-∞; -0,7] ∪ [0; 0,7];
Функция вогнута при х ∈ [-0,7; 0] ∪ [0,7; +∞)
x перегиба = {-0,7; 0; 0,7}
Строим график: