1)Решение системы неравенств [-2, (-1+√73)/4]
2)Решение системы неравенств х∈(0,2, 1)
Объяснение:
1. Решите систему неравенств:
3х+4≤4х+6
х-5≤4-2х²
Во втором неравенстве перенесём все члены уравнения в левую часть, приравняем к нулю и решим, как квадратное уравнение:
х-5-4+2х²≤0
2х²+х-9=0
х₁,₂=(-1±√1+72)/4
х₁,₂=(-1±√73)/4
х₁=(-1-√73)/4 ≈ -9,5
х₂=(-1+√73)/4 ≈ 7,5
Начертим СХЕМУ параболы, которую обозначает данное уравнение (ничего вычислять не надо). Просто начертим схематично оси, параболу с ветвями вверх, и отметим на оси Ох точки х₁ ≈ -9,5 и
х₂ ≈ 7,5. Ясно видно, что у<0 при х от -9,5 до 7,5, то есть,
решение второго неравенства х∈[(-1-√73)/4, (-1+√73)/4]
Решим первое неравенство.
3х+4≤4х+6
3х-4х ≤6-4
-х ≤2
х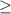
-2 знак меняется
Решение первого неравенства х∈[-2, ∞).
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств [-2, (-1+√73)/4] х от -2 до 7,5.
Неравенства нестрогие, скобки квадратные.
2. Решите двойное неравенство -3<2-5х<1
Решается как система:
2-5х>-3
2-5х<1
-5х> -3-2
-5x<1-2
-5x> -5
-5x< -1
x<1 знак меняется x ∈(-∞, 1) решение 1-го неравенства
x>0,2 знак меняется x ∈(0,2, ∞) решение 2-го неравенства
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств х∈(0,2, 1)
Неравенства строгие, скобки круглые.
В решении.
Объяснение:
а)Является ли последовательность бесконечно убывающей геометрической прогрессией если она задана формулой bn=(-4)ⁿ⁺²?
Если знаменатель |q|<1, то такая последовательность называется бесконечно убывающей геометрической прогрессией.
Значит, чтобы ответить на вопрос задания, нужно вычислить q.
b₁ = (-4)¹⁺² = (-4)³ = -64;
b₂ = (-4)²⁺² = (-4)⁴ = 256;
q = b₂/b₁
q = 256/-64
q = -4.
|q| = |-4|
|q| > 1, значит, данная прогрессия не является бесконечно убывающей геометрической прогрессией.
б)Записать бесконечную периодическую десятичную дробь 0,(12) в виде обыкновенной дроби.
Периодическая дробь — бесконечная десятичная дробь, в которой, начиная с некоторого места, стоит только периодически повторяющаяся определенная группа цифр.
0,(12) = 0,121212121212 до бесконечности.
Чтобы производить какие-то действия с периодической дробью, её нужно округлить до сотых:
0,(12) ≈ 0,12.
0,(12)=4/33.
у = 4х - 6 - линейная, хє R. (или х - любое число, или (-∞; +∞) )
у = 2х/(х-5)
Знаменатель дроби не равен нулю, поэтому
х - 5 ≠ 0
х ≠ 5
хє(-∞;5)∪(5;+∞)
(Или так: все числа, кроме 5).