
Объяснение:
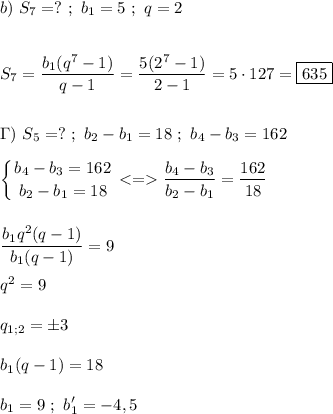
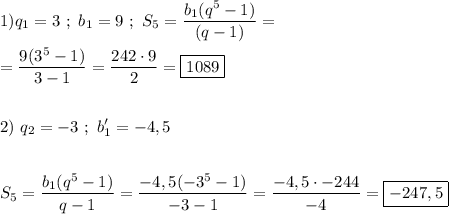
2) а) у=5. в) у=1. г) х=0. д) 8/5 или 1.6
Объяснение:
2)А)
запишем условие
у=х^4-2√х+5, чтобы найти пересечение с осью у, поставим х=0
у=0^4-2√0+5, 0 в любой положительной степени равен 0
у=0-2√0+5, любой корень из 0 равен 0
у=0-2*0+5, при добавлении или вычитании 0, величина не меняется
у=-2*0+5, любое выражение, умноженное на 0=0
у=-0+5, при добавлении или вычитании величина не меняется
у=5
2) в) условие:
у=е^х-sin x, чтобы найти пересечение с осью у, подставим х=0
у=е^0-sin(0), любое отличное от нуля выражение возведенное в степень 0 равно 1
у=1-sin(0),вычислим выражение используя таблицу тригонометрических функций
у=1-0
у=1
2) г) условие:
у=3^х*х^2, чтобы найти пересечение с осью х подставим у=0
0=3^х*х^2, поменяем местами стороны уравнений
3^х*х^2=0 если производное равно 0, то как минимум один из множителей равен нулю
3^х=0
х^2=0, решим уравнения относительно х
х( напишу словами) не принадлежит нулю
2^х=0, х=0, найти объединение
х=0
2) д) условие:
у=√5х-8, чтобы найти пересечение с осью х, подставим у=0
0=√5х-8, поменяем местами стороны уравнения
√5х-8=0, корень может быть равным 0 только в одном случае, если подкоренное выражение равно 0
5х-8=0, перенести постоянную в правую часть и сменить ее знак
5х=8, разделим обе стороны уравнения на 5
х=8/5, проверим, является ли данное значение решением уравнения
0=√5*5/8-8, упростим
0=0, равенство верно, следовательно х=8/5 и является решением уравнения
P.S можно также записать в виде десятичной дроби, получится 1.6
Прости зайка, 3 не знаю как делать(
Надеюсь то что я сделала тебе удачи)
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
б)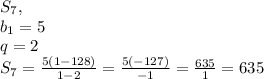
г)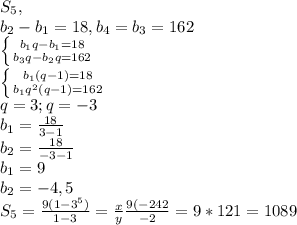
Объяснение: