17
Объяснение:
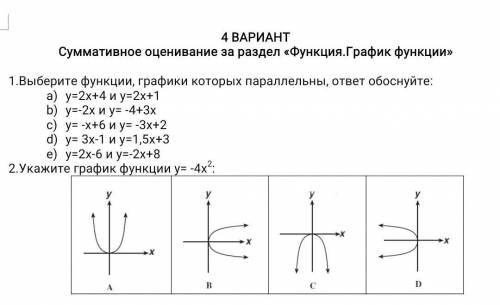
Попробуем угадать исходную функцию. Рассмотрим слагаемое 21x. Пусть в исходной функции перед x стоял коэффициент C₁. Тогда 2C₁x - (-C₁x) = 3C₁x = 21x ⇒ C₁ = 7. Рассмотрим модули. Заметим, что |-x + a - 5| = |x - a + 5|. Пусть в исходной функции содержалось выражение C₂|x + a - 5| + C₃|x - a + 5|. Тогда для полученных коэффициентов составим систему:
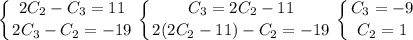
Свободный член не зависит от x, поэтому если в исходной функции было выражение C₄(-8a + 28), то в выражении оно равно 2C₄(-8a + 28) - C₄(-8a + 28) = C₄(-8a + 28) = -8a + 28 ⇒ C₄ = 1.
Значит, 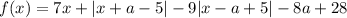 . График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
. График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
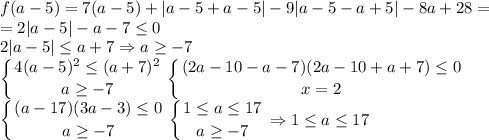
Наибольшее значение параметра — 17.

Приведем подобные члены. Я их сгруппирую для наглядности:
Различия между ними - это степень и сама буква неизвестного значения: "a" и "b".
Далее просто складываем и вычитаем в зависимости от знака подобные члены. Все упрощение, условно, сводится в 3 действия, так как 3 вида значений:
1)
2)
3)
В итоге записываем полученное выражение:
На этом можно остановиться, можно вынести одинаковые значения за общую скобку. Этим значением является буква b, тогда запись выражения примет вид:
Но нужно помнить, что когда мы выносим одинаковые члены за скобку, то от чего мы их отделяем - делим на то самое отделяемое значение. Если расписать действие переноса буквы b за скобку по шагам, то будет более понятно:
Решение без пояснений:
---------------------------------------------------------------------
2.
Тут самое главное правильно раскрыть скобки с учетом знаков перед ними, а далее все как в первом решении. Начинать раскрытие скобок нужно изнутри, то есть от выражения "
Распишу раскрытие скобок по действиям:
1)
2)
3)
В итоге получили выражение под пунктом 3.
Далее, приводя подобные члены получим:
Далее можем также вынести за скобку одинаковые члены, но в этом нет смысла, так как не принесет упрощения.
Решение без пояснений: