Объяснение:
Координаты точки пересечения можно найти методом вычитания:
а)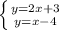 
чтобы найти переменную 
, достаточно вычесть от верхней части системы нижнюю, тогда получится 
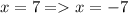, найдем координату 
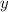, подставим значение х в любую часть системы: 
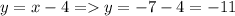, следовательно точка пересечения этих прямых будет находится по координатам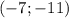 
б)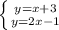 
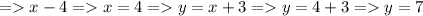, искомый ответ будет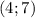 
в)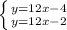 
тут возникает противоречие, если прямые вычесть, то мы не сможем найти или 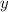, или же будет 
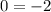, что не является верным, значит прямые не будут пересекаться, они являются параллельными
г)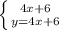 
тут уже можно сразу найти 
, искомый ответ будет 
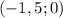
ответ: а)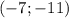, б)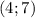, в)Нет решения, г)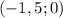
Примечание: Если в г была система такая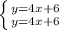 
, то это это две прямые, которые совпадают и ответом будет бесконечное множество.
x-8)(p+x)≤0, p∈N,
x^2+(p-8)x-8p≤0,
a=1>0,
x^2+(p-8)x-8p=0,
D=(p-8)^2-4*(-8p)=(p+8)^2>0,
x_1=(-(p-8)-(p+8))/2=-p,
x_2=(-(p-8)+(p+8))/2=8,
-p≤x≤8, x∈[-p;8];
a) x_2=x_1+9,
-p+9=8,
p=1,
-1≤x≤8, x∈[-1;8]; /-1, 0, 1, 2, 3, 4, 5, 6, 7, 8
б) -3<x_1≤-2,
-3<-p≤-2,
2≤p<3,
p=2,
-2≤x≤8, x∈[-2;8]; /-2, -1
в) -4<x_1≤-3,
-4<-p≤-3,
3≤p<4,
p=3,
-3≤x≤8, x∈[-3;8]; /-3, -2, -1, 0
г) x_1>0,
-p>0,
p<0, p∉N
^ - возведение в степень, ^2 - в квадрате, ^3 - в кубе, ^(10) - в 10 степени
_ - нижний индекс, х_1 - х первое, х_2 - х второе
20m
2)x^2+2xy+y^2-x^2+2xy-y^2
4xy
3)36-12n+n^2-n^2-12n-36
-24n
4)4p^2-4pm+m^2-m^2-4pm-4p^2
-8pm
5)x^2-12x+36-9x^2
-8x^2-12+36 (тут можно решить как квадратное уравнение)
6)4y^2-y^2-6y-9
3y^2-6y-9 тут тоже(3y^2-6y-9=0) если не проходили то не надо