10. Два велосипедиста выехали с места старта по кольцевому маршруту од- новременно в противоположных направлениях. Первому велосипедисту, кото-
рый ехал быстрее второго, после первой встречи нужно было ехать 1,8 км до
места старта, а второму велосипедисту после второй встречи нужно было ехать
0,4 км до места старта. Найдите длину кольцевого маршрута.
3
11*. Два спортсмена выбегают одновременно с места старта в одном направ-
лении по дорожке стадиона длиной 400 м со скоростями 16,8 и 17 км/ч. Сколько
метров до места старта придется бежать более быстрому спортсмену, когда рас-
стояние между спортсменами первый раз станет равным 20 м?
12. Водитель хотел проехать весь путь с одной скоростью за некоторое вре-
мя. Однако, передумал и часть пути проехал со скоростью на 20 % больше, чем
собирался ехать, а остальную часть пути со скоростью на 20 % меньше, чем со-
бирался в самом начале. В итоге получилось, что на весь путь он затратил такое
же время, что и планировал в начале. Какую часть пути водитель проехал с
меньшей скоростью?
13. Коля ехал в поезде со скоростью 76 км/ч, а Толя ехал по встречному пу-
ти. Расстояние между Колей и Толей дважды было равно 16 км, сначала через
5 ч после начала поездки Коли, а затем через 5 ч 12 мин после начала этой по-
ездки. С какой скоростью ехал Толя?
14. Водитель собирался проехать от одного города до другого с некоторой
постоянной скоростью за некоторое время. Если эту скорость увеличить на
20 %, то на весь путь ушло бы на полчаса меньше времени. А если скорость
уменьшить на 10 км/ч, то на весь путь ушло бы на 3
8
ч больше времени, чем
предполагалось. Найдите расстояние между городами.
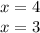
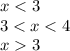
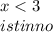
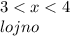
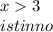
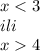
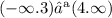
х*y*z=231
Разложим число 231 на множители:
3*7*11=231
По условиям задачи количество квартир на каждом этаже больше 2, но меньше 7, т.е. 2> у <7
Отсюда видно, что число квартир равное 7 или 11 не подходит, т.к. не будет выполняться неравенство. Неравенство выполняется, если количество квартир на этаже равно 3:
2> 3 <7 (Значит 7 и 11 квартир быть не может).
Количество квартир у =3
Пусть число этажей z=7 (11 подъездов), тогда количество квартир в подъезде составляет 3*7=21
первый подъезд имеет счет квартир: с 1 по 21
второй подъезд: с 22 по 42
Не подходит, т.к. не выполняется условие задачи: во втором подъезде есть квартира номер которой больше 42. Если число этажей 7, а число квартир 3, тогда максимальный номер квартиры во втором подъезде 42.
Возьмем количество этажей равным z=11, тогда количество квартир в подъезде 11*3=33
1 подъезд: с 1 по 33 номер
2 подъезд: с 34 по 66 номер (больше 42).
Выполнены все условия задачи.
Значит, в доме 11 этажей, 7 подъездов и 3 квартиры на каждом этаже.
ответ: 11 этажей.