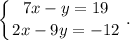
Выразим в первом уравнении переменную "у". Для этого нужно перенести неизвестную в правую часть и сменить ее знак. Получим:
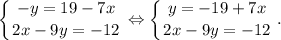
Подставим данное значение "у" в уравнение "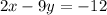 ". Получим:
". Получим:
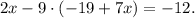
Рапределяем "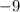 " через скобки. Получим:
" через скобки. Получим:
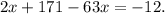
Приводим подобные члены. Получим:
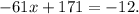
Переносим постоянную в правую часть и сменяем ее знак. Получим:
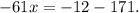
Вычисляем разность. Получим:
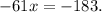
Делим обе стороны уравнения на "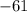 ". Получим:
". Получим:
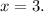
Подставляем данное значение "х" в уравнение "у=-19+7х". Получим:
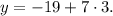
Умножаем числа. Получим:
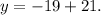
Вычисляем сумму. Получим:
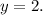
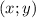 "
" 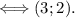
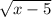 больше или равно 0, потому что нельзя извлечь квадратный корень из отрицательного числа. значит чтобы найти область определения, надо найти все иксы, при которых этот корень ≥0. вот это и запишем
больше или равно 0, потому что нельзя извлечь квадратный корень из отрицательного числа. значит чтобы найти область определения, надо найти все иксы, при которых этот корень ≥0. вот это и запишем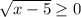
Объяснение:
у=-1/2х^2+х-1
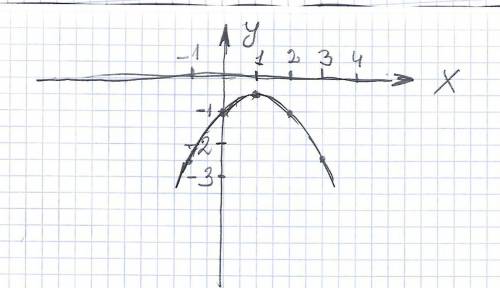
Коэффициент перед х² отрицательный,значит ветви параболы направлены вниз. Число по модулю меньше 1. значит парабола "шире" параболы Х².Парабола имеет максимум.находим точки на оси Х.
у=0=-1/2х^2+х-1 *2
0=-х²+2х-2 ищем корни (-2±√(4-4*(-1)(-2))/(2*(-1)) =(-2±√(-4))/(-2)корней нет. Значит парабола целиком ниже оси Х.
Х вершины равен -в/2а=-1/(-1)=1
У вершины равен У=-1/2+1-1 =-1/2
(1;-1/2) вершина.
Строим таблицу х -1 0 1 2 3
у -2,5 -1 -0,5 -1 -2,5
Точка пересечения с осью У при Х=0 у= 0+0-1 =-1 (0;-1)
Теперь наносим эти точки на оси координат и соединяем плавной кривой. Свойства. Возрастает при х∠1 ,убывает при 1∠х .
отрицательна при всех значениях Х. вершина-точка максимума.
Объяснение:
В первом уравнении выразим переменную y через переменную x и подставим полученное выражение во второе уравнение вместо y:
Раскроем скобки и приведем подобные:
Подставим найденное значение переменной x в первое уравнение и найдем значение переменной y: