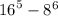
мальчиков пересадить нельзя
Объяснение:
175*2=350 - значит все парты заняты и свободных мест нет.
Поскольку половина всех девочек сидит с мальчиками, то вторая половина девочек сидит друг с другом, т.е. 1/2*1/2=1/4 всех девочек. Т.е. число девочек должно быть кратно 4.
Если мы аналогичным образом рассадим мальчиков, то мальчиков также должно быть количество кратное 4.
Значит количество учеников школы можно представить как:
(х+у)*4=350
350:4= 87 ( ост. 2) т.е. нацело не делится, а значит мальчиков не может быть количество кратно 4. Следовательно мальчиков так пересадить нельзя.
Теорема. Конечное объединение счетных множеств дает счетное множество.
По сути нужно доказать, что 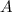и 
и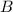 
являются счетными. Докажем счетность множества .
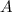Очевидно, что между каждым элементом множества 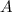можно поставить взаимоднозначное соответствие с множеством натуральных чисел, которое как известно является счетными, т.е. множество 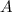- счетно.
Докажем теперь счетность множества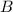
Согласно основной теореме алгебры, полином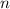 
-ой степени имеет 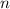различных корней, т.е., очевидно, что количество полиномов является счетным, поскольку для каждого полинома можно установить биекцию множеству натуральных чисел, причем каждый полином имеет конечное число корней, тогда по выше сказанной теореме множество 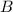- счетно.
Следовательно,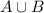 
- счетно.
Кратно 3 получилось :(