Question

периметр садового участка прямоугольной формы равен 160м,а его площадь равна 1596м2. найти длину меньшей стороны участка!

Answer 1

Объяснение:

Пусть длина участка равна х м., а ширина - у м. Зная, что периметр = 160 м, а формула для нахождения периметра P=2*(a+b) и площадь участка = 1596 м^2 а формула S=a*b, составим систему уравнений:

$\left \{ {{2*(x+y)=160} \atop {x*y=1596}} \right.$$\left \{ {x+y=160:2} \atop {x*y=1596}} \right.$$\left \{ {x+y=80} \atop {x*y=1596}} \right.$$\left \{ {x=80-y} \atop {x*y=1596}} \right.$

Выразив одну величину через другую, выполним подстановку и решим уравнение с одним неизвестным, получим :

(80-у)*у=1596

80у-у^2=1596

y^2-80y+1596=0

D=b^2-4ac=80^2-4*1*1596=6400-6384=16 D>0, уравнение имеет 2 корня:

у1,2=(-b±√D)/2a

y1=(80-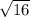$\sqrt{16}$)/2*1=(80-4)/2=76/2=38

y2=(80+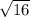$\sqrt{16}$)/2*1=(80+4)/2=84/2=42

Тогда х1+38=80

х1=80-38=42

х2+42=80

х2=80-42=38. Значит размеры садового участка равны 38 м и 42 м, меньший из них равен 38 м