Исходный график:
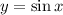
Растягиваем в два раза от оси y. Получим:
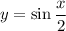
Выполняем симметрию относительно оси y. Получаем:
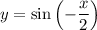
Выполняем сдвиг на п/6 единиц направо. Получаем:
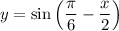
Растягиваем в 2 раза от оси х. Получаем:
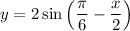
Выполняем симметрию относительно оси y. Получаем:
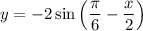
Выполняем сдвиг на 3 единицы вверх. Получаем искомый график:
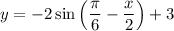
Цепочку рассуждений можно упростить, если воспользоваться нечетностью функции синуса и преобразовать исходную функцию:
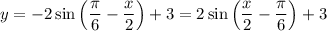
Тогда алгоритм действий будет следующий:
- растяжение в 2 раза от оси x
- сдвиг на п/6 единиц вправо
- растяжение в 2 раза от оси y
- сдвиг на 3 единицы вверх
Найдем ОДЗ (Область допустимых значений). Т.к. на ноль делить нельзя, знаменатель не должен быть равен 0. Отсюда находим:
Дальше можно решить разными
Решим методом интервалов (более удобен):
Отмечаем точки ОДЗ и решения на координатной прямой, находим знаки для каждого промежутка и находим решение неравенства (см. прикрепленный рисунок).
P.S. Незакрашенные точки значат, что это значение не входит в промежуток (обозначается круглой скобочкой), а закрашенные - наоборот (обозначается квадратной скобочкой).
Решим с правила расщепления:
Т.е. существуют два случая, при которых частное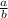
может быть ≥ 0 (Нужно использовать >, < вместо ≥, ≤ соответственно для знаменателя, поскольку он не может быть равен 0):
Т.е. решением является совокупность (нас устраивает и то, и другое решение):
Зная это правило, решаем неравенство:
Решим, для удобства, неравенства отдельно.
Первое:
Возможны два случая, когда произведение a × b может быть ≥ 0:
Т.е. решением является совокупность (нас устраивает и то, и другое решение):
Второе:
Возможны два случая, когда произведение a × b может быть ≤ 0:
Т.е. решением является совокупность (нас устраивает и то, и другое решение):
Вернемся к решению другой совокупности:
Учитывая ОДЗ, найдем решение:
Теперь решим другое неравенство.
Зная, что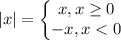
разделим наше неравенство на 4 системы: