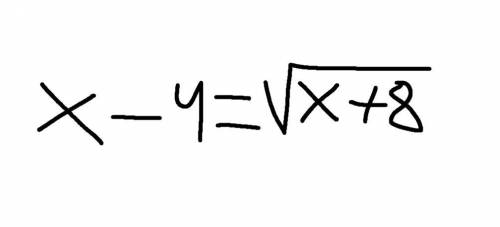
Государственный флаг Республики Казахстан представляет собой прямоугольное полотнище голубого цвета с изображением в центре солнца с лучами, под которым – парящий орел. У древка – вертикальная полоса с национальным орнаментом. Изображение солнца, его лучей, орла и национального орнамента – цвета золота.
Автор Государственного флага Республики Казахстан – заслуженный деятель искусств Казахстана Шакен Ниязбеков.
Государственный герб Республики Казахстан
Государственный герб Республики Казахстан имеет форму круга и представляет собой изображение шанырака на голубом фоне, от которого во все стороны в виде солнечных лучей расходятся уыки. Справа и слева от шанырака расположены изображения мифических крылатых коней. В верхней части расположена объемная пятиконечная звезда, а в нижней части надпись «Қазақстан». Изображение звезды, шанырака, уыков, мифических коней, а также надписи «Қазақстан» – цвета золота.
Авторами Государственного герба Республики Казахстан являются известные архитекторы Жандарбек Малибеков и Шот-Аман Валиханов.
Государственный гимн Республики Казахстан
Гимн Казахстана, ранее известный как песня «Менің Қазақстаным», по инициативе Президента Нурсултана Назарбаева был утвержден Парламентом страны 6 января 2006 года. Впервые он прозвучал 11 января 2006 года во время торжественной инаугурации Главы государства.
Музыка – композитора Шамши Калдаякова, слова – Жумекена Нажимеденова и Нурсултана Назарбаева
Система лінійних рівнянь із двома змінними:
a) {x - y = 1
2x - y = 6
б) {5x + y = 4
y = 3 - x
в) {x^2 + y^2 = 4
x^2 + y^2 = 5
x^2 - y^2 = -3
Знайдемо координати точок перетину графіка рівняння х + 2у = 4 з осями координат:
а) (0;2), (4;0)
б) (2;1), (-2; 1)
в) (1;2)
г) (1; -2)
Для знаходження точок перетину з осями координат, підставимо в рівняння відповідні значення:
а) Підставляємо (0;2) в рівняння:
0 + 2(2) = 4
4 = 4
Отже, точка (0;2) задовольняє рівняння х + 2у = 4.
Підставляємо (4;0) в рівняння:
4 + 2(0) = 4
4 = 4
Отже, точка (4;0) також задовольняє рівняння х + 2у = 4.
б) Підставляємо (2;1) в рівняння:
2 + 2(1) = 4
4 = 4
Отже, точка (2;1) задовольняє рівняння х + 2у = 4.
Підставляємо (-2;1) в рівняння:
-2 + 2(1) = 4
0 = 4 (Неправильно)
Отже, точка (-2;1) не задовольняє рівняння х + 2у = 4.
в) Підставляємо (1;2) в рівняння:
1 + 2(2) = 4
5 = 4 (Неправильно)
Отже, точка (1;2) не задовольняє рівняння х + 2у = 4.
г) Підставляємо (1;-2) в рівняння:
1 + 2(-2) = 4
-3 = 4 (Неправильно)
Отже, точка (1;-2) не задовольняє рівняння х + 2у = 4.
Отже, з варіантів, набір точок перетину графіка рівняння х + 2у = 4 з осями координат відповідає варіанту А) (0;2), (4;0).
x - 4 = √( x + 8)
ограничения
x + 8 ≥ 0 x ≥ -8
x - 4 ≥ 0 x ≥ 4
x ∈ [4, +∞)
так части положительны то в квадрат смело
(x - 4)² = x + 8
x² - 8x + 16 = x + 8
x² - 9x + 8 = 0
D = 81 - 32 = 49
x₁₂ = (9 ± 7)/2 = 1 8
x = 1 < 4 нет
x = 8 > 4 да
ответ х = 8
8 - 4 = √(8 + 8)
4 = √16
4 = 4