x = 5, y = 2
Объяснение:
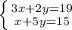
Метод сложения — это когда мы делаем так, чтобы можно было сократить одно из неизвестных в системе. То есть, нам нужно умножить одно из уравнений на такое число, чтобы при сложении с другим уравнением сократилось одно неизвестное (x или y)
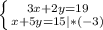
Я умножил нижнее уравнение на -3, потому что сверху у меня стоит неизвестное 3x, а чтобы его сократить, надо его сложить с -3x
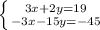
Складываем уравнения, то есть часть, находящуюся слева от равно первого уравнения прибавляем к левой части второго, так же и с правыми частями:
3x + 2y - 3x - 15y = 19 - 45
-13y = -26
y = 2
Подставляем полученный y в одно из уравнений, например, в первое:
3x + 2*2 = 19
3x = 15
x = 5
y'=2x+4/x-2;
2x+4/x-2=0;
x1=-2;
x2=2; - выколотая точка;
y=0; значит:
точка (-2;0) - экстремиум функции;
методом интервалов находим убывание/возрастание:
убывает: (-беск;-2]
возрастает: [-2;+беск)
ищем асимптоты:
слева: lim(x->-беск)(x+2/x-2)^2;
справа: lim(x->беск)(x+2/x-2)^2;
эти пределы равны:
=x+2/x-2=1+0/1-0=1;
значит уравнение горизонтальной асимтоты и слева и справа: y=1;
наклонные асимтоты совпадают с горизонтальными;
пересекает ох при х=-2; (-2;0)
оу при у=1; (0;1)
берем еще несколько точек и строим график