Пусть первая цифра трехзначного числа будет - а. Вторая - в Третья -с. Тогда должно выполнятся равенство 5*а*в*с=100*а+10*в+с Проанолизировав равенство получаем, что: 1)а≠0,в≠0 и с≠0 так как иначе 5*а*в*с=0 а это совсем не трехзначное число 2) с=5 Так как любое число умноженное на 5 ( 5*а*в*с ) будет оканчиватся 0 или 5 (а нуль мы уже исключили в первом пункте) 3) а и в - должны быть нечетные, так как иначе число 5*а*в*с=25*а*в будет оканчиваться нулем (если а-четное то его можно представить в виде а=2к. Значит 25*а*в=25*2*к*в=100*в, оканчивается нулем противоречит с первому) Подставим в равенство с=5 и получим значение а через в 5*а*в*с=100*а+10*в+с 25*а*в=100*а+10*в+5 25*а*в-100а=10*в+5 а(25в-100)=10*в+5 а=(10*в+5)/(25в-100) а=(2*в+1)/(5в-20) При всех в<5 Знаменатиль будет меньше или равен нулю. Поэтому эти варианты не рассматриваем. Остаются толко нечетные варианты при в=5 : а=(2*5+1)/(5*5-20)=11/5 не подходит (так как это не целочисленное решение) при в=7 : а=(2*7+1)/(5*7-20)=15/15=1 подходит при в=9 : а=(2*9+1)/(5*9-20)=19/25 не подходит Единственное решение - 175
Здесь первый корень можно путем сложения коэффициентов, если при сложении получается 0, то один из корней равен 0. t=1 1+1-2=0 Значит один из множителей (t-1). Проведем деление многочленов. _t⁸+t-2 I t-1 t⁸-t⁷ t⁷+t⁶+t⁵+t⁴+t³+t²+t-2 _t⁷+t t⁷-t⁶ _t⁶+t t⁵- t⁴ _ t⁴+t t⁴- t³ _t³+t t³- t² _t²+t t² -t _ 2t-2 2t-2 0
(t⁷+t⁶+t⁵+t⁴+t³+t²+t-2)(t-1)=0
Если мы посмотрим на уравнение 8 степени, то можно увидеть, что чем больше число (+ или -), тем дальше значение уравнения от 0. Значит надо искать корни в пределах [-1;1]. t⁷+t⁶+t⁵+t⁴+t³+t²+t-2 - действительных корней не имеет. Значит t=1
![\sqrt[8]{x-2}=-(x-2)+2 \\ \\ \sqrt[8]{x-2}+(x-2)-2=0 \\ \\ \sqrt[8]{x-2}=t](/tpl/images/0290/7987/57e05.png)
1) x = ±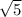
2) y =±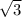
3) z = ±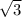
4) k = ±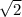
5) x1 = ±1; x2 = ±3
6) y = ±1
7)t1 = ±1; t2 = ±2
8)x1 = ±3; x2 = ±0.5
Объяснение:
1) x^4 - x^2 - 20 = 0
Замена x^2 = t >0
t^2 - t - 20 = 0
D = 1 + 4*20 = 81 = 9^2
t1 = (1 + 9)/2 = 5
t2 = (1 - 9)/2 = -4 - посторонний
Обратная замена
x^2 = 5
x = ±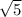
2)y^4 - 6y^2 + 9 = 0
Замена y^2 = t >0
t^2 - 6t + 9 = 0
D = 36 - 4*9 = 0
t = (6 ± 0)/2 = 3
Обратная замена
y^2 = 3
y = ±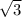
3) z^4 - z^2 - 6 = 0
Замена z^2 = t >0
t^2 - t - 6 = 0
D = 1 + 4*6 = 25 =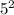
t1 = (1 + 5)/2 = 3
t2 = (1 - 5)/2 = -2 - посторонний
Обратная замена
z^2 = 3
z = ±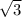
4) x^4 - 10x^2 + 9 = 0
Замена x^2 = t >0
t^2 - 10t + 9 = 0
т.к. a + b + c = 0
t1 = 1
t2 = 9
Обратная замена
x^2 = 1 или x^2 = 9
x1 = ±1
x2 = ±3
4) k^4 + 5k - 14 = 0
Замена k^2 = t >0
t^2 + 5t - 14 = 0
D = 25 + 4*14 = 81
t1 = (-5 + 9)/2 = 2
t2 = (-5 - 9)/2 = -7 - посторонний
Обратная замена
k^2 = 2
k = ±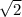
6) 49y^4 - 48y^2 - 1 = 0
Замена y^2 = t >0
49t^2 - 48t - 1 = 0
т.к. a + b + c = 0
t1 = 1
t2 = -1 - посторонний
Обратная замена
y^2 = 1
y = ±1
7) t^4 - 5t^2 + 4 = 0
Замена t^2 = x >0
x^2 - 5x + 4 = 0
т.к. a + b + c = 0
x1 = 1
x2 = 4
Обратная замена
t^2 = 1 или t^2 = 4
t1 = ±1
t2 = ±2
8) 4x^4 - 37x + 9 = 0
Замена x^2 = t >0
4t^2 - 37t + 9 = 0
D = 1369 - 4*4*9 = 35²
t1 = (37 + 35)/8 = 9
t2 = (37 - 35)/8 = 0.25
Обратная замена
x^2 = 9 или x^2 = 0.25
x1 = ±3
x2 = ±0.5