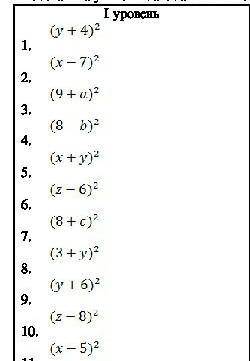
Формулы: 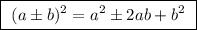 .
.
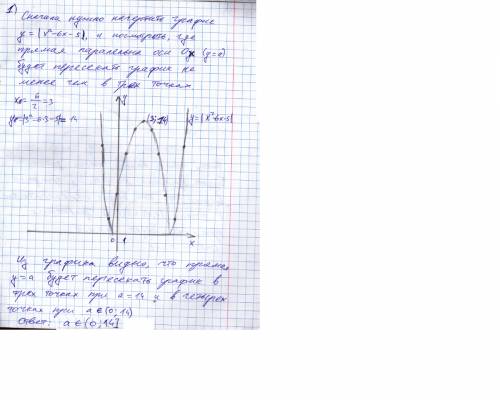
1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,
а нижнее а=0.
находим вершину параболы, х0=-b/2a у нам b=6 a=-1 x0=3
y0=-9+5+18=14
значит а [0;14]
2) sqrt(x-1)=a+x x>=1
x-1=x^2+a^2+2ax
x^2+(2a-1)x+a^2+1=0
D>0 (2a-1)^2-4a^2-4>0 -4a-3>0 a<-3/4
3) 4x^2-15x+4a^3=0
x1=x2^2
x1*x2=a^3
x2^3=a^3 x2=a
15/4=x1+x2 15/4=a^2+a
4a^2+4a-15=0 a1=3/2 a2=-5/2
x^2-ax+(a-1)=0
x1^2+x2^2=(x1+x2)^2-2x1x2=17
a^2-2(a-1)=17
a^2-2a-15=0
a1=5 a2=-3



Нужно воспользоваться формулой разности квадратов практически во всех примерах: (a - b)(a + b) = a² - b².
Выполните умножение:
1) 5b(b - 1)(b + 1) = 5b(b² - 1) = 5b³ - 5b;
2) (c + 2)(c - 2) · 8c² = (c² - 4) · 8c² = 8c⁴ - 32c²;
3) (m - 10)(m² + 100)(m + 10) = (m - 10)(m + 10)(m² + 100) =
= (m² - 100)(m² + 100) = m⁴ - 10 000;
4) (a² + 1)(a² - 1)(a⁴ + 1) = (a⁴ - 1)(a⁴ + 1) = a⁸ - 1;
Упростите выражение:
1) (x + 1)(x - 1) - (x + 5)(x - 5) + (x + 1)(x - 5) = x² - 1 - (x² - 25) + x² - 5x + x - 5 = x² - 1 - x² + 25 + x² - 4x - 5 = x² - 4x + 19;
2) 81a⁸ - (3a² - b³)(9a⁴ + b⁶)(3a² + b³) = 81a⁸ - (3a² - b³)(3a² + b³)(9a⁴ + b⁶) = 81a⁸ - (9a⁴ - b⁶)(9a⁴ + b⁶) = 81a⁸ - (81a⁸ - b¹²) = 81a⁸ - 81a⁸ + b¹² = b¹².
1. (у+4)² = у²+8у+16
2. (х-7)² = х²-14х+49
3. (9+а) = 81+18а+а²
4. Знака нету, делаю с «+» и «-»
(8-b)² = 64-16b+b²
(8+b)² = 64+16b+b²
5. (x+y)² = x²+2xy+y²
6. (z-6)² = z²-12z+36
7. (8+c)² = 64+16c+c²
8. (3+y)² = 9+6y+y²
9. (y+6)² = y²+12y+36
10. (z-8)² = z²-16z+64
11. (x-5)² = x²-10x+25