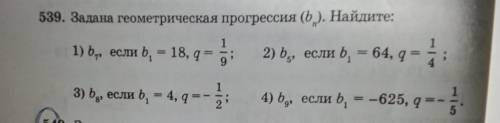
формула энного члена геометрической прогрессии bn=b₁*qⁿ⁻¹, где b₁ ее первый член, q - знаменатель прогрессии ;
1) b₇=18*(1/9)⁶=2/9⁵=2/59049
2) b₅=64*(1/4)⁴=64/(4*64)=1/4,
3) b₈=4*(-1/2)⁷=4/(-128)=-1/32,
4) b₉=-625*(-1/5)⁸=-625/390625=-1/625
а) x² + 4x + 10 ≥ 0
D = 4² - 4· 10 = - 24
График функции у = x² + 4x + 10 - парабола веточками вверх, пересечения с осью Ох нет, т.к. D < 0, поэтому у > 0 и ответ
2) Решением неравенства является вся числовая прямая
b) -x² + 10x - 25 > 0
-(х - 5)² > 0
Поскольку -(х - 5)² < 0 при любых х, то ответ
1) Неравенство не имеет решений
c) x² + 3x + 2 ≤ 0
D = 3² - 4 · 2 = 1
x₁ = 0.5(-3 - 1) = -2
x₂ = 0.5(-3 + 1) = -1
График функции у = x² + 3x + 2 - парабола веточками вверх, пересекает ось Ох в точках с координатами x₁ = -2 и x₂ = -1 поэтому решением неравенства является интервал [-2; -1] , и ответ
4) Решением неравенства является закрытый промежуток.
d) -x² + 4 < 0
x² - 4 > 0
График функции у = x² - 4 - парабола веточками вверх, пересекает ось Ох в точках с координатами x₁ = -2 и x₂ = 2 поэтому решением неравенства является интервалы (-∞; -2) и (2; +∞) , и ответ
6) Решением неравенства является объединение двух промежутков
Объяснение:



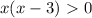
 ∈
∈ 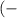 ∞
∞  ∪
∪ 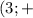 ∞
∞ 

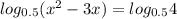
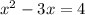
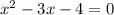
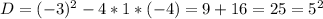
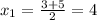
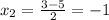



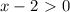
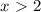
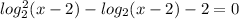

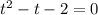

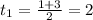

 или
или 
 или
или 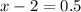
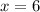 или
или 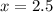

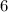
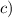
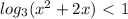

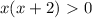
 ∈
∈ 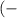 ∞
∞  ∪
∪ 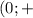 ∞
∞ 

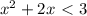


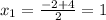

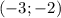 ∪
∪ 
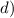










Формулa: bₙ=b₁*qⁿᐨ¹
539.
1)
Дано: b₁=18⠀⠀⠀q=1/9
Найти: b₇
b₇=b₁*q⁶
b₇=18*(1/9)⁶=18/531 441 = 2/59049
2)
Дано: b₁=64⠀⠀⠀q=1/4
Найти: b₅
b₅=b₁*q⁴
b₅=64*(1/4)⁴=64 * 1/256=1/4
3)
Дано: b₁=4⠀⠀⠀q= -1/2
Найти: b₈
b₈=b₁*q⁷
b₈=4*(-1/2)⁷= -4 * 1/128 = - 1/32
4)
Дано: b₁= -625⠀⠀⠀q= -1/5
Найти: b₉
b₉=b₁*q⁸
b₉= -625*(-1/5)⁸= - 625/390 625 = - 1/625