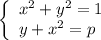
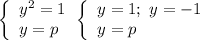
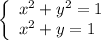
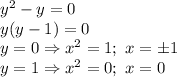
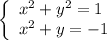
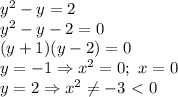
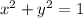 - окружность с центром в точке (0; 0) и радиусом 1
- окружность с центром в точке (0; 0) и радиусом 1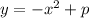 - стандартная парабола ветвями вниз с вершиной в точке
- стандартная парабола ветвями вниз с вершиной в точке
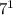 и заметить, что простое число в какой-либо степени имеет число делителей на 1 больше чем его показатель степени.
и заметить, что простое число в какой-либо степени имеет число делителей на 1 больше чем его показатель степени.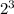 имеет 4 делителя. Так, как 3+1=4
имеет 4 делителя. Так, как 3+1=4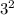 имеет 3 делителя. Так, как 2+1=3
имеет 3 делителя. Так, как 2+1=3
a) 6x^2-15x-2x+5
б) 3х^2 -26x - 35 -(10x^2- 18x -4)= 3x^2 -26x-35 -10x^2 + 18x + 4=
= -7x^2 + 8x -31
в) (5x^2 - 21x-4) * (x+2)= 5x^3 - 11x^2 - 38x - 8
2) (2x+6) * (7-4x) = (2-x)*(8x+1)+ 15
-10x-8x^2+42 = 15x - 8x^2 +2+15
42-2-15=25x
25=25x
x=1