
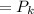 , то остается вычислить вероятности того сколько самолётов собют системы ПВО.
, то остается вычислить вероятности того сколько самолётов собют системы ПВО.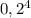
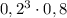
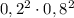
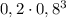
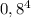 - логика подсказівает, что если самолеты были сбиты системой ПВО то соответствующая вероятность попадания
- логика подсказівает, что если самолеты были сбиты системой ПВО то соответствующая вероятность попадания 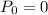 но как по мне это не наше дело, нам ничего не мешает оставить это слагаемое в формуле, в результате получим:
но как по мне это не наше дело, нам ничего не мешает оставить это слагаемое в формуле, в результате получим: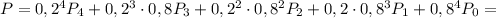
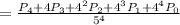
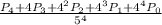
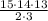
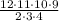
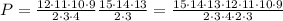
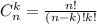
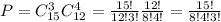
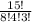
Для решения воспользуемся равносильным переходом.
Решим первое уравнение системы и затем на тригонометрической окружности пересечем с неравенством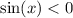 .
.
*окружность с проверкой корней прикреплена*