Объяснение:
Задание 2.
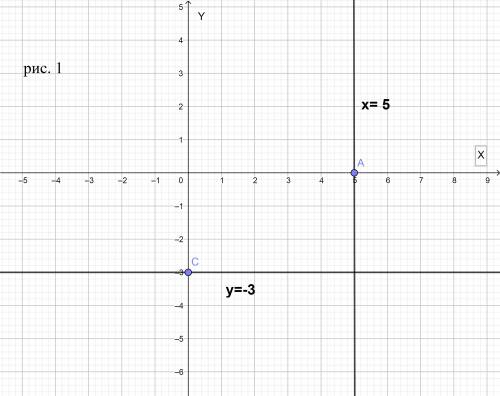
а) Координату х=5 будут иметь все точки , лежащие на прямой , которая параллельна оси ординат и проходит через т.А на оси абсцисс. Любая другая точка координатной плоскости имеет абсциссу отличную от х=5
б) Координату у=-3 будут иметь все точки , лежащие на прямой , которая параллельна оси абсцисс и проходит через т.С на оси ординат. Любая другая точка координатной плоскости имеет ординату отличную от у=-3
рисунок 1 во вложении
Задание 3.
а) На координатной плоскости неравенство х ≥ 4 задаст полуплоскость , которая будет расположена правее прямой х=4. Все точки этой полуплоскости будут иметь абсциссу равную 4 и больше
рисунок 2 во вложении
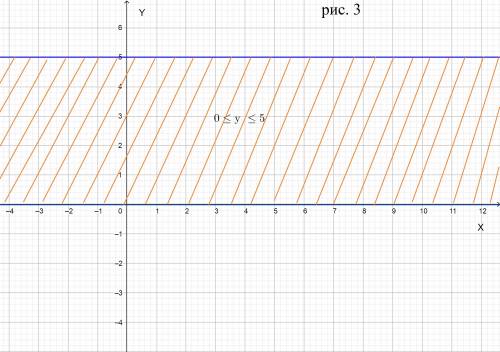
б) Двойное неравенство 0 ≤ у ≤ 5 задает на координатной плоскости две горизонтальные полосы , которые имееют ординату 0 и 5
рисунок 3 во вложении
Задание 4.
а) у = х;
найдем точки и построим график
х=0, у=0
х=3 , у=3
х=-3, у= -3
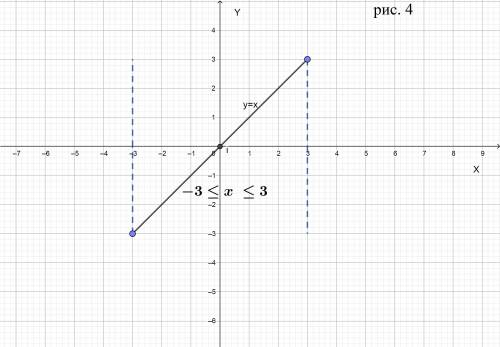
б) –3 ≤ х ≤ 3.
неравенство задает на координатной плоскости две вертикальные полосы, которые имею абсциссу 3 и -3
Изобразим множество точек на координатной плоскости
рисунок 4 во вложении
Задание 5
Решение во вложении
Задание 6
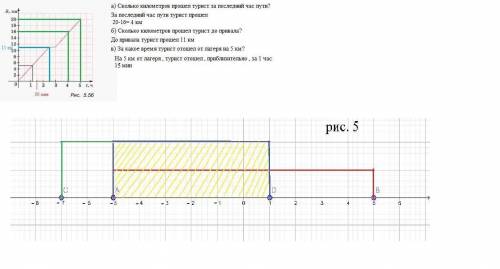
Если | x | ≤ 5 , значит -5 ≤ х ≤ 5, т.е. х ϵ [-5 ; 5]
Отметим этот промежуток т.А и т.В на координатной прямой ( рис. 5 во вложении)
Отметим промежуток –7 ≤ x ≤ 1 , т.е. х ϵ [ -7 ; 1] на координатной прямой т.С и т. D
Для того, чтобы определить границы промежутков [-5; 5] и [-7; 1] сравним левые и правые границы этих промежутков. Поскольку -7 < -5, а 5 >1 , то искомое пересечение имеет вид: х ϵ[-5; 1]

Объяснение:
Задание 2.
а) Координату х=5 будут иметь все точки , лежащие на прямой , которая параллельна оси ординат и проходит через т.А на оси абсцисс. Любая другая точка координатной плоскости имеет абсциссу отличную от х=5
б) Координату у=-3 будут иметь все точки , лежащие на прямой , которая параллельна оси абсцисс и проходит через т.С на оси ординат. Любая другая точка координатной плоскости имеет ординату отличную от у=-3
рисунок 1 во вложении
Задание 3.
а) На координатной плоскости неравенство х ≥ 4 задаст полуплоскость , которая будет расположена правее прямой х=4. Все точки этой полуплоскости будут иметь абсциссу равную 4 и больше
рисунок 2 во вложении
б) Двойное неравенство 0 ≤ у ≤ 5 задает на координатной плоскости две горизонтальные полосы , которые имееют ординату 0 и 5
рисунок 3 во вложении
Задание 4.
а) у = х;
найдем точки и построим график
х=0, у=0
х=3 , у=3
х=-3, у= -3
б) –3 ≤ х ≤ 3.
неравенство задает на координатной плоскости две вертикальные полосы, которые имею абсциссу 3 и -3
Изобразим множество точек на координатной плоскости
рисунок 4 во вложении
Задание 5
Решение во вложении
Задание 6
Если | x | ≤ 5 , значит -5 ≤ х ≤ 5, т.е. х ϵ [-5 ; 5]
Отметим этот промежуток т.А и т.В на координатной прямой ( рис. 5 во вложении)
Отметим промежуток –7 ≤ x ≤ 1 , т.е. х ϵ [ -7 ; 1] на координатной прямой т.С и т. D
Для того, чтобы определить границы промежутков [-5; 5] и [-7; 1] сравним левые и правые границы этих промежутков. Поскольку -7 < -5, а 5 >1 , то искомое пересечение имеет вид: х ϵ[-5; 1]





Пусть событие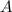 - "выпало 6 очков", а событие
- "выпало 6 очков", а событие 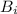 - "было произведено i бросков".
- "было произведено i бросков".
Предполагается, что количество бросков определяется случайно, то есть:
В данном случае конкретное числовое значение не столь важно, главное что оно одинаково для всех гипотез.
Для решения задачи понадобится формула Байеса:
Нам нужно найти вероятность того, что был 1 бросок, при условии того, что выпало 6 очков:
Распишем полную вероятность:
Найдем вероятности выпадения 6 очков при 1, 2, 3, 4 бросках.
При одном броске вероятность выпадения 6 очков, как и любого другого количества очков:
При двух бросках, 6 очков может выпасть в следующих комбинациях:
{1; 5} - 2 вариант
(3; 3) - 1 вариант
{4; 2} - 2 вариант
Благоприятных вариантов - 5. Общее количество вариантов выпадения комбинации на двух кубиках равно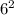 .
.
При трех бросках, 6 очков может выпасть в следующих комбинациях:
{1; 1; 4} - 3 варианта
(1; 2; 3) - 6 вариантов
Благоприятных вариантов - 9.Общее количество вариантов выпадения комбинации на трех кубиках равно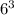 .
.
При четырех бросках, 6 очков может выпасть в следующих комбинациях:
{1; 1; 1; 3} - 4 варианта
(1; 1; 2; 2) - 6 вариантов
Благоприятных вариантов - 10.Общее количество вариантов выпадения комбинации на четырех кубиках равно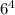 .
.
Таким образом, искомая вероятность:
ответ: 54/115