Объяснение:
1.Функция -отношение между элементами, при котором изменение в одном элементе влечёт изменение в другом.Область определения функции-множество, на котором задаётся функция.
2. Начальная функция это y0. Неопределенный интеграл-это совокупность всех первообразных данной функции.
Свойства неопределенного интеграла
1)Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
2)Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
3)Постоянный множитель можно вынести из-под знака интеграла, т.е. если то
4)Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности, т.е.
Интегрирование- название, данное ряду приемов, используемых для вычисления различных ИНТЕГРАЛОВ.
3.

![\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}+\dfrac{4}{9\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}}+\dfrac{2}{3}](/tpl/images/1351/8334/f1fa1.png)
Объяснение:
Найдем дискриминант кубического уравнения:
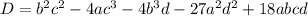
У нас:
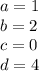
Теперь это нужно посчитать:
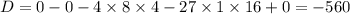
Поскольку D<0, то уравнение имеет 1 вещественный корень.
Выделим полный куб из выражения.
Предварительно вспомним, что 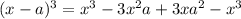 .
.
У нас:
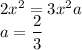
Тогда, учитывая, что 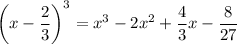 , получим:
, получим:
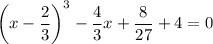
А теперь вынесем 4/3 за скобки:
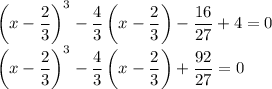
Теперь можно делать замену вида 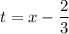 .
.
Получим:
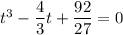
Мы привели уравнение к виду, где отсутствует член со 2-ой степенью неизвестного. Первый этап выполнен.
Второй этап будет заключаться в сведении полученного уравнения к квадратному.
Выполним новую замену:
![t=\sqrt[3]{q}+\dfrac{4}{9\sqrt[3]{q}}](/tpl/images/1351/8334/d6860.png)
Тогда получим:
![\left(\sqrt[3]{q}+\dfrac{4}{9\sqrt[3]{q}}\right)^3-\dfrac{4}{3}\left(\sqrt[3]{q}+\dfrac{4}{9\sqrt[3]{q}}\right)+\dfrac{92}{27}=0](/tpl/images/1351/8334/c3a6d.png)
Посчитав это получим:
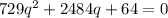
Решив это уравнение через дискриминант получим:
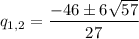
Берем один любой q.
Я возьму 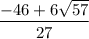 .
.
Выполним обратную замену:
![t=\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}+\dfrac{4}{9\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}}](/tpl/images/1351/8334/f60fb.png)
Выполним вторую обратную замену:
![x=\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}+\dfrac{4}{9\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}}+\dfrac{2}{3}\approx-1,1304](/tpl/images/1351/8334/f1ebf.png)
Уравнение решено!
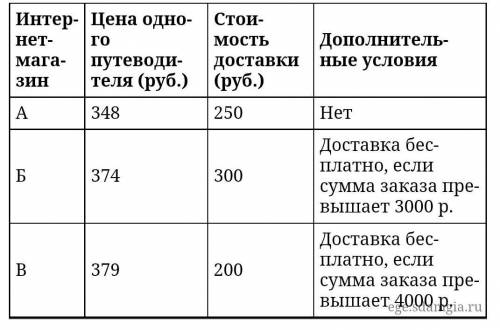
Б
Объяснение:
Вариант А (348*10)+(250*10) = 5 980
Вариант Б 374 = 3740 сума заказа превышает 3000р
Вариант В (379*10)+(200*10)= 5 790 доставка платная т.к заказ не превышает 4000р