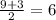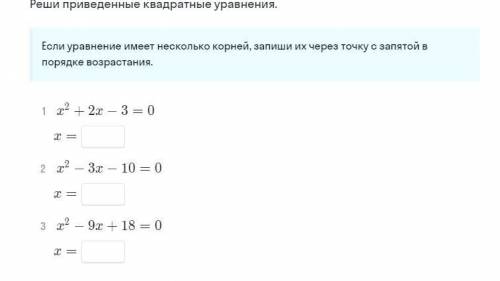
Пусть купили n карандашей за 5 рублей. Тогда остаток c равен:
c = 50 - 5n
Отсюда зависимость c от n выражается формулой:
c(n) = 50 - 5n
Найдём область определения:
n - это целое неотрицательное число(неотрицательное так как мы не можем купить -1 карандаш и целое, потому что мы не можем взять, к примеру, 2,4 карандаша), то есть n ≥ 0
Также остаток не может быть меньше нуля:
50 - 5n ≥ 0
5n ≤ 50
n ≤ 10
Область определения: 0 ≤ n ≤ 10
Следовательно число точек равно 10 - 0 + 1 = 11 точек
График этой функции в приложении
Пусть скорость пешехода х км/ч, а велосипедиста — (х+10) км/ч. Пусть встреча произошла на расстоянии у от В. АВ = 4 км - по условию, ВС=у.
АСВ
велосипедист проехал АВ+ВС = 4+у за время (4+у) /х+10,
а пешеход АВ - ВС = 4-у за время (4-у) /х, что равно 24 мин = 2/5 часа.
Система: (4+у) /x+10 = 2/5,
(4-y) / x = 2/5. Запиши в виде дробей и перемножь накрест, как в пропорциях.
Найди у.
2х=20-5у (1) х=20-5у/2
(2) 2х+20=20+5у
Из (1) в (2) подставим 20-5у/2 вместо х:
(2): 2(20-5у/2)+20=20+5у
10у=20
у= 2
подставляем 2 в (1)
х=20-10/2=5 км/ч
скорость пешехода
1)
x₁ = -3
x₂ = 1
2)
x₁ = -2
x₂ = 5
3)
x₁ = 3
x₂ = 6
Объяснение:
До решения пара пояснений:
- квадратное уравнение имеет вид:
ах² + bx + c = 0
- все уравнения буду решать через дискриминант
- формула дискриминанта: b² - 4ac
- формула корней:
x₁ =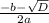
x₂ =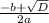
1) х² + 2х - 3 = 0
D = 4 - 4 * 1 * (-3) = 4 + 12 = 16
x₁ =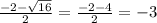
x₂ =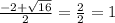
2) x² - 3x -10 = 0
D = 9 - 4 * 1 * (-10) = 9 + 40 = 49
x₁ =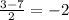
x₂ =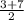
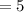
3) x² - 9x + 18 = 0
D = 81 - 4 * 1 * 18 = 9
x₁ =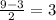
x₂ =