Выпишем простые числа от 11 до 37: 11, 13, 17, 19, 23, 29, 31, 37 Количество дробей, у которых числитель и знаменатель являются различными числами (дробь не равна 1) равно 8*7=56. Наименьшая такая дробь равна 11/37, наибольшая 37/11. Пусть в дроби x/y фиксирован числитель и равен x=a. Тогда чтобы эта дробь была больше 1/2, Знаменатель должен быть больше, чем 2a. Тогда рассмотрим каждое из чисел в качестве числителя. 1) a = 11, тогда y > 22 - из выписанных чисел таких 4 штуки. Поэтому получилось 4 дроби с числителем 11 2) a = 13, тогда y > 26 - 3 штуки 3) a = 17 => y > 34 - 1 штука 4) a = 19 => y > 38 - 0 штук Очевидно, что дальше будет так же по 0 штук. Суммируем полученные количества для каждого a и получаем 4+3+1=8 дробей, которые меньше 1/2 и у которых числитель и знаменатель составлены из перечисленных простых чисел.
Пусть двухрублевых монет х штук, а пятирублевых у штук, тогда по условию задачи 2х+5у=28. Решим это уравнение в целых числах. 2х=28-5у. В левой части чётное число, так как оно кратно 2, значит, чтобы х было целым числом, нужно, чтобы и в правой части было чётное число. Правая часть - это разность четного числа 28 и неизвестного произведения 5у. Чтобы всё выражение в правой части было четным числом, нужно, чтобы 5у было четным, так как разность двух чётных чисел есть чётное число. 5у может быть четным только если у будет четным, так как произведение чётного и нечётного есть чётное число. Получим у может быть равным либо 2, либо 4, равным 6 и более у быть не может, иначе разность 28-5у становится отрицательной. Тогда при у=2: 2х=28-5*2 => 2х=18 => х=9; при у=4: 2х=28-5*4 => 2х=8 => х=4. Значит, двухрублевых монет либо 9, либо 4 штуки. ответ: 9 или 4.
Объяснение:
Учитывая, что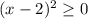
, то должны выполняться 
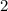неравенства:
Тогда, если данное уравнение имеет решение, то левая и правая часть уравнения должны быть равны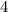
, то есть:
Если подставить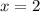
в левую часть уравнения, то равенство выполняется.
ответ: