Question

Задан график функции (см. рис.) а) Укажите, функция убывающая или возрастающая?
б) Укажите точки пересечения графика с осями координат.
в) Найдите уравнение данной функции.

Answer 1

а) Функция является убывающей, так как при движении по иску от -∞ до ∞ функция "падает" вниз.

б) Точки пересечения графика с осями: (0;4) и (2;0)

в) Уравнение прямой будем искать в виде y=kx+b:

Подставим координаты точек в равенство:

4=0•k+b, => b=4

0=2•k+4, => k=-2

Подставляем найденные b и k в уравнение прямой: y=-2x+4

Answer 2

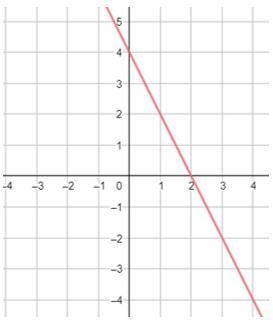
а) убывающая

б)(2;0) и (0;4)

в) Уравнение прямой определяется как y=kx+b

Выделим 2 точки и подставим их координаты в данное уравнение. Для простоты возьмём точки из пункта б

$\displaystyle \left \{ {{0=k*2+b} \atop {4=k*0+b}} \right.$

$\displaystyle \left \{ {{2k+b=0} \atop {b=4}} \right.$

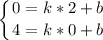
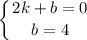
Зная, что b=4, подставим это в первое уравнение системы и решим его

$\displaystyle 2k+4=0|:2$

$\displaystyle k=-2$

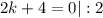
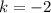
Получается уравнение прямой будет y = -2x+4