Пусть V это скорость велосипедиста из пункта А в В, тогда обрато он возвращался со скоростью V-3. S1=27 км по условию. Пусть S расстояние от А до В, тогда расстояние обрато: S-7.
10 минут нам прийдётся перевести в часа
10 мин = 10:60=1/6 ч
Пусть время, за которое он проехал из А в В будет t, тогда время, за которое он вернулся будет t-1/6.
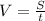
Получаем систему уравнений:
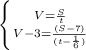
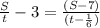
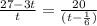
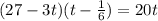
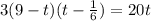
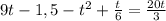
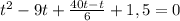
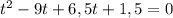
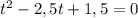 \\\получили квадратное уравнение, которое необходимо решить
\\\получили квадратное уравнение, которое необходимо решить
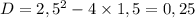
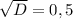
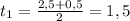 ч
ч
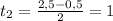 ч
ч
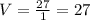 км/ч
км/ч
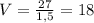 км/ч
км/ч
Получилось два возможных варианта ответа: 18 км/ч и 27 км/ч
/- дробь
1 .
(a**2-ax)/(a**2x-ax**2)
Вынесем за скобки общений множитель и получим
a(a-x)/ax(a-x)
Сократим (a-x) и a
Получаем 1/x
2. (mn**4-cn**4)/(cn**3-mn**3)
Вынесем за скобки общий множитель
n**3(mn-cn)/n**3(c-m)
Сократим на n**3
(mn-cn)/c-m
Вынесем за скобки общий множитель
n(m-c)/(c-m)
Чтобы было одно и тоже сделаем так
n(-(c-m))/(c-m)
Сократим и получим
n* (-1) = -n
3. (4p**2-16p**3)/(12**2-3p)
Вынесем общий множитель
p(4p-16p**2)/p(12p-3)
Сократим
(4p-16p**2)/p(12-3)
Вынесем общий множитель
-4p(-1+4p)/3(4p-1)
Сократим
-4p/3
Объяснение:
1) при х≥0 y=f(x)=x²-5x это квадратичная функция вершина в точке
c абсциссой х₀=-b/2a=-(-5)/2=2,5
Ордината вершины у₀=f(2,5)=2,5²-5*2,5=-6,25
Вершина в точке (2,5;-6,25) вычислим координаты нескольких точек
х 0 1 2 2,5 3 4
у 0 -4 -6 -6,25 -6 -4
2) при х<0
так как функция нечетная
f(-x)=-f(x)=-(x²-5x)=-x²+5x
f(-x)=-x²+5x
f(x)=-x²-5x
вычислим координаты нескольких точек
х -1 -2 -2,5 -3 -4
у 4 6 6,25 6 4