3*b>0 при b>0
Сумма двух положительных будет положительна, т.е a+3*b>0, если а>0 и b>0
Значит и произведение 2а*(а+3b) положительное Раскрываем скобки получаем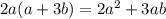 
Т.к а>0 и b>0, то a*b>0,
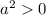для любых а.
Сумма двух положительных чисел, будет положительным числом, получаем что
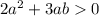при условии что a*b>0 (это возможно при a>0 и b>0, или a<0 и b<0)
Строго говоря этим мы доказали, не только что 2а(а+3b)>0 не только при а и b>0, но и при а и b<0. Т.е. чтобы выполнялось неравенство необходимо и достаточно чтобы a и b были одного знака.
Пусть одна из сторон образовавшегося прямоугольника равна х см, то другая - (24-х) см. Площадь прямоугольника вычисляются по формуле S=a*b, то S=x*(24-x)
Зададим функцию S(x)=x*(24-x), исследуем ее и найдем при каком значении она принимает наибольшее значение. S(x)=x*(24-x)=24x-x^2
D(S)=(0; 24)
S'(x)=24-2x
S'(x)=0, 24-2x=0
-2x=-24
x=12
Найдем значение производной данной функции слева S'(11)=2>0 и справа S'(13)=-2<0 от значения х=12. Значение производной меняется с + на -, значит функция в точке х=12 достигает своего максимума. Площадь прямоугольника будет наибольшей, если стороны его 12см и 12 см, т.е - квадрат