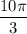![Cos^2 - sin^2 x/4 = sin (3п/2 - x), x принадлежит [3п; 3п/2]](/tpl/images/4756/3407/df4da.jpg)
Обозначим количество строк, в которых закрашена 1 клетка через a, а количество строк, в которых закрашены 7 клеток через b.
Обозначим количество столбцов, в которых закрашены 3 клетки через c, а количество столбцов, в которых закрашены 4 клетки через d.
Общее количество закрашенных красок N может быть выражено двояко:
N = a + 7b = 3c + 4d
Нам нужно найти min(N)
Имеются следующие ограничения и соотношения на a, b, c и d
a, b, c, d ∈ Z, 0 ≤ a,b,c,d ≤ 130, a + b = 130, c + d = 130
Подставим эти соотношения в равенство для N:
a + 7b = 3c + 4d
(a + b) + 6b = 3(c + d) + d
130 + 6b = 3 * 130 + d
d = 6b - 260
Т.к. 0 ≤ d ≤ 130, то:
0 ≤ 6b - 260 ≤ 130
260 ≤ 6b ≤ 390
43.(3) ≤ b ≤ 65
Т.к. нам нужно найти min(N) = min(a + 7b) = min(130 + 6b), то минимум достигается при минимальном b = 44.
Осталось построить пример, показывающий, что возможна раскраска квадрата 130*130 так, что у него будет раскрашено по 7 клеток в 44 строках, по одной клетке в 86 (130 - 44) строках, по 4 клетки в 4 столбцах (6 * 44 - 260) и по 3 клетки в 126 столбцах (130 - 4), а всего 394 клетки (86 + 7 * 44).
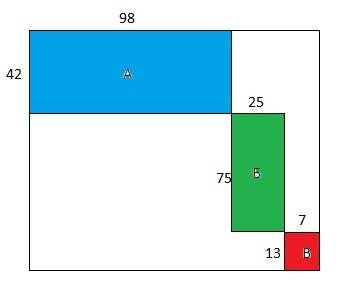
Схема заполнения квадрата показана на рис.1 - будут заполнены только прямоугольники, размеры и расположение которых указаны.
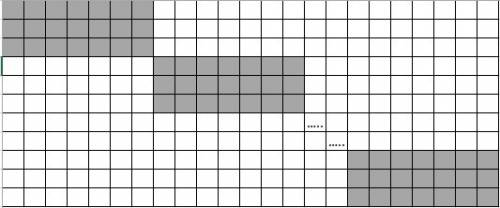
Прямоугольник А будет заполнен так, как указано на рис.2 - 14 блоков каждый размера 3 * 7.
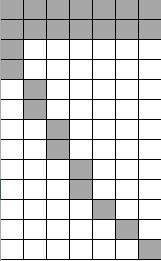
Прямоугольник Б будет заполнен так, как указано на рис.3 - 25 блоков каждый размера 3 * 1.
И наконец прямоугольник В заполнен так, как указано на рис. 3

Обозначим количество строк, в которых закрашена 1 клетка через a, а количество строк, в которых закрашены 7 клеток через b.
Обозначим количество столбцов, в которых закрашены 3 клетки через c, а количество столбцов, в которых закрашены 4 клетки через d.
Общее количество закрашенных красок N может быть выражено двояко:
N = a + 7b = 3c + 4d
Нам нужно найти min(N)
Имеются следующие ограничения и соотношения на a, b, c и d
a, b, c, d ∈ Z, 0 ≤ a,b,c,d ≤ 130, a + b = 130, c + d = 130
Подставим эти соотношения в равенство для N:
a + 7b = 3c + 4d
(a + b) + 6b = 3(c + d) + d
130 + 6b = 3 * 130 + d
d = 6b - 260
Т.к. 0 ≤ d ≤ 130, то:
0 ≤ 6b - 260 ≤ 130
260 ≤ 6b ≤ 390
43.(3) ≤ b ≤ 65
Т.к. нам нужно найти min(N) = min(a + 7b) = min(130 + 6b), то минимум достигается при минимальном b = 44.
Осталось построить пример, показывающий, что возможна раскраска квадрата 130*130 так, что у него будет раскрашено по 7 клеток в 44 строках, по одной клетке в 86 (130 - 44) строках, по 4 клетки в 4 столбцах (6 * 44 - 260) и по 3 клетки в 126 столбцах (130 - 4), а всего 394 клетки (86 + 7 * 44).
Схема заполнения квадрата показана на рис.1 - будут заполнены только прямоугольники, размеры и расположение которых указаны.
Прямоугольник А будет заполнен так, как указано на рис.2 - 14 блоков каждый размера 3 * 7.
Прямоугольник Б будет заполнен так, как указано на рис.3 - 25 блоков каждый размера 3 * 1.
И наконец прямоугольник В заполнен так, как указано на рис. 3




В левой части можно применить формулу косинуса двойного угла:
В правой части можно заменить по формуле приведения:
Тогда уравнение будет выглядеть так:
Используем формулу суммы косинусов:
В нашем случае получается:
Так как , то:
, то:
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Значит, имеем два варианта:
Теперь подбираем корни, которые принадлежат отрезку![\boldsymbol{\left[3\pi;\ \dfrac{9\pi}{2}\right]}](/tpl/images/4756/3407/76927.png) . Для этого можно решить двойное неравенство для каждой серии корней.
. Для этого можно решить двойное неравенство для каждой серии корней.
Для первой серии:
Не забываем, что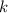 - это обязательно целое число. В данном промежутке есть только одно такое: 2. Значит,
- это обязательно целое число. В данном промежутке есть только одно такое: 2. Значит,  . Подставляем это значение в серию корней, для которой мы решали неравенство.
. Подставляем это значение в серию корней, для которой мы решали неравенство.
Одно искомое уже нашли. Теперь тем же самым образом проверим вторую серию корней.
Опять же, учитывая то, что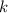 - целое число, данное неравенство НЕ ИМЕЕТ РЕШЕНИЙ, поскольку в получившемся промежутке нет целых чисел.
- целое число, данное неравенство НЕ ИМЕЕТ РЕШЕНИЙ, поскольку в получившемся промежутке нет целых чисел.
Итого мы нашли одно значение, которое одновременно и является корнем уравнения, и входит в промежуток![\left[3\pi;\ \dfrac{9\pi}{2}\right]](/tpl/images/4756/3407/d29f6.png) , а именно
, а именно  .
.
ответ: