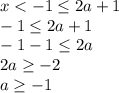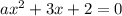

а) xp < yp
б) xp > yp
в) 1/x > 1/y
г) 1/x < 1/y
Объяснение:
а) Представь, что у тебя x = 1, а y = 2. P = любому положительному числу. Для наглядности возьмём 1.
Если ты умножишь x на p, то получишь 1 * 1 = 1. Если y умножишь на p, то получишь 2 * 1 = 2. Следовательно, у тебя произведение x и p будет меньше, чем y и p. Т.к изначально известно, что x < y.
б) Продолжаю объяснение из а. X и Y оставляем такими же: x = 1, y = 2. Однако если p - любое отрицательное число, то произведение x и p будет больше, чем y и p. Допустим, в этом примере p у нас будет = -1
Тогда получим x * p = 1 * (-1) = -1, а y * p = 2 * (-1) = -2. Тут не так определяется величина числа, как с положительными числами. В случае с отрицательными числами, больше будет то число, которое ближе к нулю. В данном примере ближе к нулю будет -1.
в) Чем меньше число на которое ты делишь, тем больше получается значение. К примеру, пусть x = 2, а y = 4. Тогда получим :
1/x = 1/2 = 0,5
1/y = 1/4 = 0,25
г) Пусть x = -2, а y = -4. тогда:
1 / (-2) = -0,5
1 / (-4) = -0,25
-0,25 > -0,5 т.к ближе к нулю.
Відповідь:
a ≥ -1
Пояснення:
Спочатку розв'яжемо подвійну нерівність. Розглянемо два можливих випадки під час розкриття модуля.
Перший: вираз під знаком модуля невід'ємний.
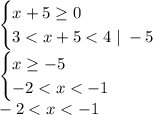
Другий: вираз під знаком модуля від'ємний
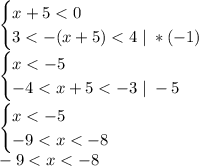
Отже, множина розв'язків цієї нерівності
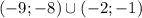
Виразимо x із нерівності з параметром:
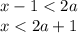
Видно, що всі розв'язки подвійної нерівності менші за -1. Тобто якщо вираз (2a+1) буде не меншим за -1, то він буде більшим і за кожний розв'язок подвійної нерівності. Інакше кажучи, підставивши замість x розв'язок нерівності 3<|x+5|<4 у нерівність x<2a+1, де 2a+1 ≥ -1 (конкретне значення), отримаємо правильне твердження. А це задовольнить умову задачі.