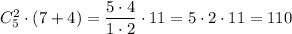
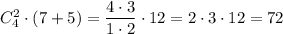
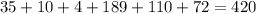
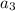 и
и 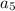 два члена, поэтому вычисляем разницу между этими членами (
два члена, поэтому вычисляем разницу между этими членами ( ) и делим на 2 (потому что какое-то число прибавлялось в два етапа: от
) и делим на 2 (потому что какое-то число прибавлялось в два етапа: от 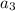 к
к 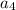 и от
и от 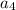 к
к 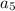 ):
):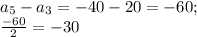 - это разность данной арифметической прогрессии.
- это разность данной арифметической прогрессии.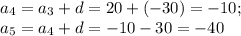 - совпадает с данными.
- совпадает с данными.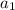 :
: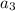 и
и 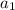 тоже два этапа, поэтому d нужно отнять два раза от
тоже два этапа, поэтому d нужно отнять два раза от 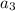 ]
]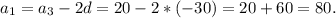
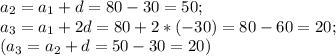 - данные совпадают.
- данные совпадают.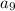 :
: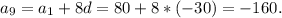
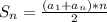 , где n - член к которому нужно считать (здесь 9).
, где n - член к которому нужно считать (здесь 9).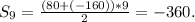
(87³+72³)/159 - 87*82 =
= (87+82)(87²-87*72+72²) /159 -87*82 =
=159(87²-87*72+72^2) / 159 - 87*82 =
=87² – 87*82 +72^2 -87*82 =
=87² -2*87*82+72²=( 87 -72)²=15²=225
*formuła: (a³+b³ ) i ( a-b)²