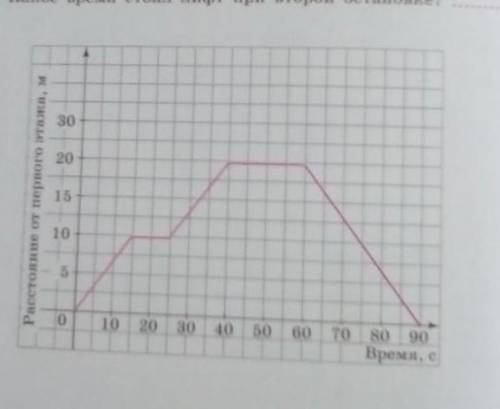
f(x) = (4x^2 + 6x + 9) / (3x)
возьмем производную :
f'(x) = ((4x^2 + 6x + 9)' * 3x - (4x^2 + 6x + 9) * (3x)')/ (3x)^2 = ((8x + 6) * 3x - (4x^2 + 6x + 9) * 3) / (9x^2) = (24x^2 + 18x - 12x^2 - 18x - 27)/(9x^2) = (12x^2 - 27)/(9x^2)
Приравняем производную к нулю и получим точки экстремума:
(12x^2 - 27)/(9x^2) = 0
12x^2 - 27 = 0
x^2 = 27/12
x = +- sqrt(27/12)
По правилу Дарбу на промежутке
(- бесконечность ; - sqrt(27/12)) функция возрастает
( - sqrt(27/12) ; 0 ) возрастает
(0 ; sqrt(27/12) ) убывает
(sqrt(27/12) ; + бесконечность) возрастает
значит точка sqrt(27/12) - точка минимума
подставим ее в уравнение и получим результат равный 6
ответ: 6
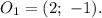
Объяснение:
Пусть точка 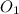 имеет координаты
имеет координаты 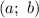 . Указаны также точки
. Указаны также точки 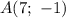 ,
, 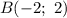 и
и 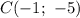 . Требуется же найти координаты точки
. Требуется же найти координаты точки 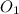 , притом таким образом, чтобы она была равноудалена от точек
, притом таким образом, чтобы она была равноудалена от точек 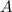 ,
,  и
и 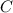 .
.
Расстояние от точки 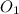 до точки
до точки 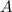 будет иметь такой вид:
будет иметь такой вид: 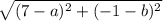 .
.
Расстояние от точки 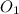 до точки
до точки  будет иметь такой вид:
будет иметь такой вид: 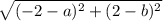 .
.
Расстояние от точки 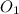 до точки
до точки 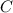 будет иметь такой вид:
будет иметь такой вид:
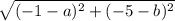 .
.
С этого момента допустимо оперировать квадратами расстояний вместо самих расстояний, так как от возведения обеих частей уравнений, которые мы получим позже, в квадрат получится полностью равносильное уравнение (ибо расстояние, очевидно, не может быть отрицательным).
Упростим все три выражения:
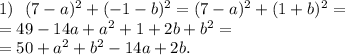
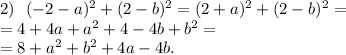
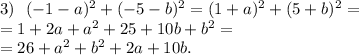
Условие же равноудалённости требует, чтобы эти три выражения были равны. Получается, что нужно решить такое уравнение:
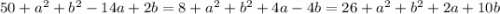 .
.
Уже здесь можно видеть, что к каждой части уравнения прибавлено выражение 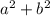 . Можно вычесть его из каждой части:
. Можно вычесть его из каждой части:
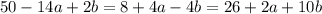 .
.
Применяя аксиому транзитивности отношения равенства (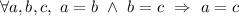 ), составим систему уравнений для нахождения
), составим систему уравнений для нахождения  и
и  :
:
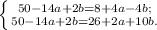
Упростим её:
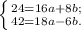
Поделим первое уравнение на 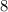 , а второе на
, а второе на 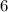 :
:
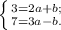
Решим систему методом сложения:
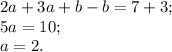
Отсюда находим  :
:
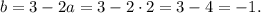
Обе координаты искомой точки найдены. ответом станет задаваемая ими точка: 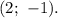
1.) 20 м
2.) 2 и 4 этажи
3.) 10сек
4.) 20сек
Объяснение:
1.) Максимальная высота - 20м
2.) Вопрос про этажи, поэтому я не могу точно ответить т. к. там всё указанно в метрах, но если считать, что 1 ед. отрезок - 1 этаж, то лифт вызывали на 2 и 4 этажи. Пока лифт стоял на этих этажах высота не менялась, а время шло.
3.) Посмотрим на время как только лифт остановился время было 15 секунд, а как только поехал время стало 25 секунд. 25-15=10(сек) - стоял лифт в первый раз
4.) Аналогично с пунктом 3 - 40сек-60сек=20(сек) - стоял лифт во второй раз