Объяснение:
Задание 1.
a)
Пусть искомые числа будут равны х и у. ⇒
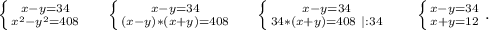
Суммируем эти уравнения:
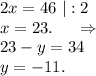
ответ: 23 и -11.
б)
Пусть сторона маленького квадрата равна х см. ⇒
Сторона большого квадрата равна (х+1) см.
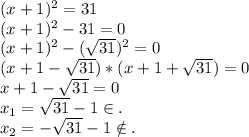
ответ: сторона маленького квадрата равна (√31-1) см.
Задание 2.
а)
Пусть последовательные натуральные числа равны х и (х+1). ⇒
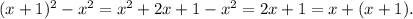
б)
Пусть последовательные натуральные числа равны х и (х+1). ⇒
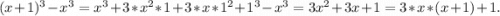
Первое слагаемое делится на 6, так как среди двух соседних натуральных чисел одно из них обязательно чётное, другое - нечётное. ⇒ Остаток всегда равен 1.
В решении.
Объяснение:
Решите задачу с составления уравнения. Разность двух чисел равна 21, а разность их квадратов 105. Найдите эти числа.
х - первое число.
у - второе число.
По условию задачи система уравнений:
х - у = 21
х² - у² = 105
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 21 + у
(21 + у)² - у² = 105
441 + 42у + у² - у² = 105
42у = 105 - 441
42у = -336
у = -336/42
у = -8 - второе число.
х = 21 + у
х = 21 + (-8)
х = 13 - первое число.
Проверка:
13 - (-8) = 13 + 8 = 21, верно.
13² - (-8)² = 169 - 64 = 105, верно.
Пусть доля кислоты в первом сосуде - х, тогда масса кислоты в первом сосуде - 30х кг. Пусть доля кислоты во втором сосуде - у, тогда масса кислоты во втором сосуде - 20х кг.
// Составим уравнения:
30х + 20у = 50 * 0.68 = 34;
20х + 20у = 40 * 0.7 = 28;
// Решим систему уравнений, вычтя второе из первого:
/30х + 20у = 34;
\20x + 20y = 28;
10x = 6 => x = 0.6 (значит доля кислоты в первом сосуде - 60%);
// подставим найденный х, чтобы найти у:
20 * 0.6 + 20у = 28;
12 + 20у = 28;
20у = 16 => у = 0.8 (значит доля кислоты во втором сосуде - 80%);
Чтобы узнать сколько килограммов кислоты находится в первом сосуде необходимо перемножить вес раствора из первого сосуда на долю, то есть:
30 * 0.6 = 18 (кг) - кислоты в первом сосуде;
Чтобы узнать на сколько % масса воды во втором растворе меньше массы кислоты, необходимо вычислить массу воды и кислоты:
20 * 0.8 = 16 (кг) - кислоты во втором сосуде;
20 - 16 = 4 (кг) - воды во втором сосуде;
4 / 16 = 0.25 = 25% - доля массы воды от массы кислоты;
100 - 25 = 75 - на столько % масса воды меньше массы кислоты;
ответ: 18 кг, на 75%.