


Объяснение:
Обозначим за Х количество мест в ряду в 1-м зале
Тогда (Х+10) - количество мест в ряду во 2-м зале
420/Х - количество рядов в 1-м зале
480/(Х+10) - количество рядов во 2-м зале
420/Х-480/(Х+10)=5
приводим левую часть уравнения к общему знаменателю и складываем:
(420Х+4200-480Х)/Х(Х+10)=5
(4200-60Х)/(Х²+10Х)=5
делим обе части уравнения на 5:
(840-12Х)/(Х²+10Х)=1, или имеем право записать как:
840-12Х=Х²+10Х
Х²+22Х-840=0
Решая полученное квадратное уравнение, находим, что:
Х₁=20
Х₂=-42 данный корень не удовлетворяет условию задачи, поскольку количество мест в ряду не может быть отрицательным.
20 мест в ряду в 1-м зале
30 мест в ряду во 2-м зале (на 10 мест больше, чем в ряду первого зала)
21 ряд в 1-м зале
16 рядов во 2-м зале (на 5 рядов меньше, чем в первом зале
 - время, за которое разгружает машину первый грузчик, мин;
- время, за которое разгружает машину первый грузчик, мин; - время, за которое разгружает машину второй грузчик, мин;
- время, за которое разгружает машину второй грузчик, мин;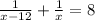 - время, за которое разгружают машину оба грузчика, мин;
- время, за которое разгружают машину оба грузчика, мин;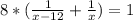
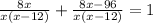
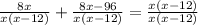
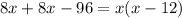
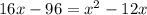
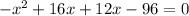
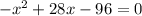

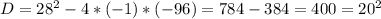
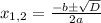
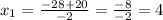
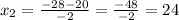
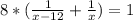
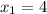 не подходит, так как время не может быть отрицательным. Следовательно ответ 24.
не подходит, так как время не может быть отрицательным. Следовательно ответ 24.
Задание 1.
Выберем в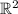 стандартный базис (то есть векторы
стандартный базис (то есть векторы 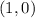 и
и 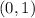 ). В
). В 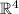 выбираем тоже стандартный базис. Образы базисных векторов:
выбираем тоже стандартный базис. Образы базисных векторов: 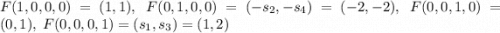 . Здесь уже есть два линейно независимых вектора:
. Здесь уже есть два линейно независимых вектора: 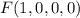 и
и 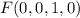 , а потому
, а потому 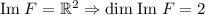 (а базис приведен чуть выше). Теперь ясно какая размерность ядра:
(а базис приведен чуть выше). Теперь ясно какая размерность ядра: 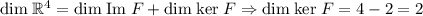 . Элементы ядра должны удовлетворять системе
. Элементы ядра должны удовлетворять системе 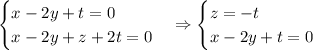 . Уже отсюда можно было понять, что размерность ядра равна двум: четыре переменные и два уравнения, ограничивающие их. Тогда положив
. Уже отсюда можно было понять, что размерность ядра равна двум: четыре переменные и два уравнения, ограничивающие их. Тогда положив 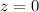 , получим, например, решение
, получим, например, решение 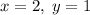 , а для
, а для 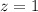 подойдет
подойдет 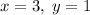 . Итого два вектора:
. Итого два вектора: 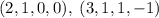 . Линейная независимость этих векторов гарантирует, что они являются базисом ядра.
. Линейная независимость этих векторов гарантирует, что они являются базисом ядра.
Задание 2.
Чтобы показать, что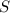 является базисом в
является базисом в 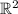 достаточно показать, что она линейно независима (достаточно, поскольку вектора два, а размерность
достаточно показать, что она линейно независима (достаточно, поскольку вектора два, а размерность 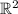 равна двум). В нашем случае система состоит из одного вектора
равна двум). В нашем случае система состоит из одного вектора  и потому не может быть базисом в
и потому не может быть базисом в 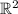 . Часть 2 решить все-таки не могу, поскольку
. Часть 2 решить все-таки не могу, поскольку 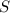 -- не базис.
-- не базис.
Задание 3.
(A)
(B)
Поскольку размерность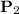 равна трем, то для того чтобы показать, что
равна трем, то для того чтобы показать, что 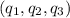 -- базис, достаточно показать, что они линейно независимы. Это легко видеть хотя бы потому, что ранг матрицы
-- базис, достаточно показать, что они линейно независимы. Это легко видеть хотя бы потому, что ранг матрицы  равен трем (поскольку ее определитель, равный
равен трем (поскольку ее определитель, равный 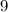 , ненулевой).
, ненулевой).
Задание 4.
В нашем случае имеем систему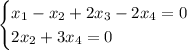 . Количество решений зависит от размерности пространства, которое задает данная система. По сути, можно рассматривать отображение
. Количество решений зависит от размерности пространства, которое задает данная система. По сути, можно рассматривать отображение 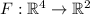 такое, что
такое, что 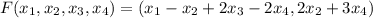 . Тогда система задает ядро этого отображения, размерность которого в новой интерпретации ищется просто -- точно так же, как мы делали это в первой задаче. Образы базисных векторов:
. Тогда система задает ядро этого отображения, размерность которого в новой интерпретации ищется просто -- точно так же, как мы делали это в первой задаче. Образы базисных векторов: 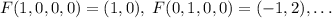 дальше считать не стал, поскольку уже первые два вектора линейно независимы. Значит, размерность образа равна двум, но тогда ядро имеет размерность
дальше считать не стал, поскольку уже первые два вектора линейно независимы. Значит, размерность образа равна двум, но тогда ядро имеет размерность 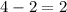 . Следовательно, ядро как множество бесконечно (было бы конечным только в случае нульмерного ядра). То есть имеем две свободные переменные. Например, систему можно свести к
. Следовательно, ядро как множество бесконечно (было бы конечным только в случае нульмерного ядра). То есть имеем две свободные переменные. Например, систему можно свести к 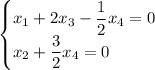 , тогда переменные
, тогда переменные 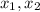 будут базисными, а
будут базисными, а 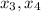 -- свободными. Ненулевое решение предъявить просто:
-- свободными. Ненулевое решение предъявить просто: 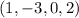 Пространство решений есть ядро
Пространство решений есть ядро 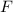 , а поскольку его размерность два, нам достаточно найти два линейно независимых решений системы. Одно мы уже нашли. Теперь положим
, а поскольку его размерность два, нам достаточно найти два линейно независимых решений системы. Одно мы уже нашли. Теперь положим 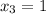 и тогда
и тогда 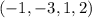 -- решение. Но это два линейно независимых решения, а потому они образуют базис пространства решений.
-- решение. Но это два линейно независимых решения, а потому они образуют базис пространства решений.
Задание 5.
1. В нашем случае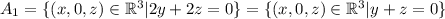 . Легко видеть, что берутся числа вида
. Легко видеть, что берутся числа вида 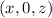 , то есть
, то есть 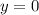 и потому
и потому 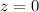 , значит,
, значит, 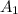 состоит из тех и только тех чисел, у которых две последние координаты нулевые. Следовательно,
состоит из тех и только тех чисел, у которых две последние координаты нулевые. Следовательно, 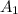 является подпространством, потому что это множество замкнуто относительно суммы (
является подпространством, потому что это множество замкнуто относительно суммы (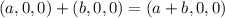 ) и умножения на скаляр.
) и умножения на скаляр.
2.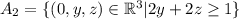 . Несмотря на то что это множество замкнуто относительно суммы, оно не замкнуто относительно умножения на скаляр. В самом деле, например,
. Несмотря на то что это множество замкнуто относительно суммы, оно не замкнуто относительно умножения на скаляр. В самом деле, например, 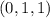 лежит в множестве, однако
лежит в множестве, однако 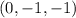 -- не лежит. Следовательно, это множество не является подпространством.
-- не лежит. Следовательно, это множество не является подпространством.
3.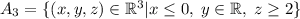 . Здесь те же причины:
. Здесь те же причины: 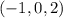 лежит в множестве, а
лежит в множестве, а 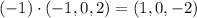 -- нет.
-- нет.