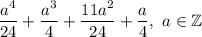
Преобразуем выражение:
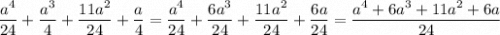
Рассмотрим и преобразуем числитель:
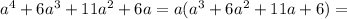
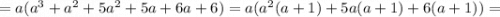
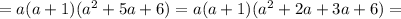
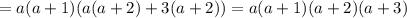
Получилось произведение четырех подряд идущих целых чисел.
Из четырех подряд идущих целых чисел гарантированно найдется хотя бы одно, кратное 3. Также, из четырех подряд идущих целых чисел найдется два четных числа, одно из которых не только четное, но и кратно 4.
Таким образом, в произведении гарантированно есть множители 3, 2 и 4. Тогда, такое произведение делится на 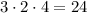 .
.
Запишем:
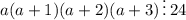
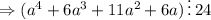
В исходной дроби такое выражение как раз делится на 24. Как выясняется, это выражение кратно 24. Значит, результат деления на 24 будет целым числом:
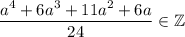
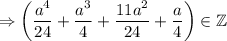
Доказано.
Стороны были равны n и 6n . После увеличения первой и уменьшения второй первая стала 3*n= 3n, и вторая 6:2n= 3n. то есть получился квадрат со стороной 3n
Периметр был (n+6n)*2 =14n, стал 4*3n=12n
Площадь прямоугольника была n*6n =6n^2, а стала 3n*3n=9n^2, то есть площадь увеличилась в полтора раза
Если же вопрос стоит тоько о площажи, то изменеие ее можно посчитать как произведение изменений сторон, то есть
S2 = S1*3/2 = 1.5 S1